4. Some RCT Examples#
4.1. Polio RCT#
One of the earliest randomized experiments were the Polio vaccination trias conducted by the Public Health Service in 1954. The question was whether Salk vaccine prevented polio. Children in the study were randomly assigned either a treatment (polio vaccine shot) or a placebo (saline solution shot), without knowing which one they received. The doctors in the study, making the diagnosis, did not know whether a child received a vaccine or not. In other words, the trial was a double-blind, randomized control trial. The trial had to be large, because the rate at which Polio occured in the population was 50 per 100,000. The treatment group saw 33 polio cases per 200,745; the control group saw 115 cases per 201,229. The estimated avearage treatment effect is about $\( -40 \)\( with the 95% confidence band (based on approximate normality of the two sample means and their differences): \)\([-52, -28].\)$ As this is an RCT, the confidence band suggests that the Polio vaccine caused the reduction in the risk of polio.
The interesting thing here is that we don’t need the underlying individual data to evaluate the effectivess of the vaccine. This is because the outcomes are Bernoulli random variables, and we have enough information to compute the estimate of ATE as well as the confidence intervals from the group case counts.
We also compute the Vaccine Efficacy metric, which refers to the following measure according to the CDC: $\( VE = \frac{\text{Risk for Unvaccinated - Risk for Vaccinated}}{\text{Risk for Unvaccinated}}. \)$ It describes the relative reduction in risk caused by vaccination.
It is staighforward to get the VE estimate by just plugging-in the numbers, but how do we get the approximate variance estimate? I am too lazy to do calculations for the delta method, so I will just use a simulation (a form of approximate bootstrap) to obtain the confidence intervals.
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
NT = 200745 #number of treated
NC = 201229 #number of controlled
YT = 33/NT #average outcome for treated
YC =115/NC #average outcome for controlled
#incidence per 100000
print("Incidence per 100000 among treated:" + str(YT*100000))
print( "Incidence per 100000 among controlled:"+ str(YC*100000))
# treatment effect estimate reduction in incidence per 100000 people
delta_hat = 100000*(YT-YC)
print("Estimate TE of occurances per 100,000 " + str(100000*(YT-YC)))
Var_delta_hat = (100000**2)*(YT*(1-YT)/NT + YC*(1-YC)/NC)
# standard deviation
print("Standard deviation for ATE"+ str(Var_delta_hat**.5))
# here we are using the fact that outcomes are Bernoulli
CI_delta = [delta_hat -1.96*Var_delta_hat**.5, delta_hat +1.96*Var_delta_hat**.5]
print("95 % confidence interval is [" + str(CI_delta[0]) + ","+
str(CI_delta[1]) + "]" )
# Here we calculate the overall effectiveness of the vaccine and construct confidence intervals for it
NV = 200745;
NU = 201229;
RV = 33/NV;
RU = 115/NU;
VE = (RU - RV)/RU;
print("Overall VE is "+ str(VE) )
# this recovers the number in the table.
# we set up a simulation example.
# calulate variance of risk estimates:
Var_RV = RV*(1-RV)/NV
Var_RU = RU*(1-RU)/NU
# set-up MC draws:
B = 10000
RVs = RV + np.random.normal(0, 1, B)*(Var_RV)**.5
RUs = RU + np.random.normal(0, 1, B)*(Var_RU)**.5
VEs= (RUs - RVs)/RUs
CI_VE_L = np.quantile(VEs, .025)
CI_VE_U = np.quantile(VEs, .975)
print("95 % confidence interval is [" + str(CI_VE_L), ",",
str(CI_VE_U), "]" )
from sklearn.neighbors import KernelDensity
import matplotlib
import matplotlib.pyplot as plt
from scipy.stats import norm
from sklearn.neighbors import KernelDensity
from sklearn.utils.fixes import parse_version
# instantiate and fit the KDE model
X= VEs[:, np.newaxis]
X_plot = np.linspace(0, 1, 1000)[:, np.newaxis]
kde = KernelDensity(kernel='gaussian', bandwidth=0.02).fit(X)
log_dens = kde.score_samples(X_plot)
plt.fill_between(X_plot[:, 0], np.exp(log_dens))
Incidence per 100000 among treated:16.438765598146905
Incidence per 100000 among controlled:57.14882049803955
Estimate TE of occurances per 100,000 -40.71005489989265
Standard deviation for ATE6.047412320702958
95 % confidence interval is [-52.56298304847044,-28.85712675131485]
Overall VE is 0.7123516206478694
95 % confidence interval is [0.5894864168097469 , 0.8153931322097857 ]
<matplotlib.collections.PolyCollection at 0x7f12db15de10>
4.2. Pfizer/BNTX Covid-19 RCT#
Here is a link to the FDA briefing and an interesting discussion, as well as data.
Pfizer/BNTX was the first vaccine approved for emergency use to reduce the risk of Covid-19 decease. In studies to assess vaccine efficacy, volunteers were randomly assigned to receive either a treatment (2-dose vaccination) or a placebo, without knowing which they recieved. The doctors making the diagnoses did not know now whether a given volunteer received a vaccination or not. The results of the study are given in the following table :
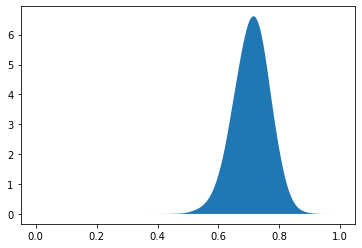
Here we see both the overall effects and the effects by age group. The confidence intervals for the averal ATE are tight and suggest high effectiveness of the vaccine. The confidence intervals for the age group 65-75 are much wider. We could group 65-75 and >75 groups to evaluate the effectiveness of the vaccine and also narrow down the width of the confidence band.
In this case, the reported results are for vaccine effectiveness. We use the same approach as above.
In the code cell below we calculate the overall effectiveness of the vaccie and construct confidence intervals for it.
NV = 19965;
NU = 20172;
RV = 9/NV;
RU = 169/NU;
VE = (RU - RV)/RU;
print("Overall VE is "+ str(VE))
# this recovers the number in the table.
# we set up a simulation example.
# calulate variance of risk estimates:
Var_RV = RV*(1-RV)/NV
Var_RU = RU*(1-RU)/NU
# set-up MC draws:
B = 10000
RVs = RV + np.random.normal(0, 1, B)*(Var_RV)**.5
RUs = RU + np.random.normal(0, 1, B)*(Var_RU)**.5
VEs= (RUs - RVs)/RUs
CI_VE_L = np.quantile(VEs, .025)
CI_VE_U = np.quantile(VEs, .975)
print("95 % confidence interval is [" + str(CI_VE_L), ",",
str(CI_VE_U), "]" )
from sklearn.neighbors import KernelDensity
import matplotlib
import matplotlib.pyplot as plt
from scipy.stats import norm
from sklearn.neighbors import KernelDensity
from sklearn.utils.fixes import parse_version
# instantiate and fit the KDE model
X= VEs[:, np.newaxis]
X_plot = np.linspace(0, 1, 1000)[:, np.newaxis]
kde = KernelDensity(kernel='gaussian', bandwidth=0.02).fit(X)
log_dens = kde.score_samples(X_plot)
plt.fill_between(X_plot[:, 0], np.exp(log_dens))
Overall VE is 0.9461934124362605
95 % confidence interval is [0.9087121000335966 , 0.9806032696306969 ]
<matplotlib.collections.PolyCollection at 0x7f12db15df10>

In the code cell below we calculate the effectiveness of the vaccine for the two groups that are 65 or older
# Here we calculate the overall effectiveness of the vaccine for the two groups that are 65 or older
NV = 3239+805;
NU = 3255+812;
RV = 1/NV;
RU = (14+5)/NU;
VE = (RU - RV)/RU;
print("Overall VE is "+ str(VE))
# this recovers the number in the table.
# we set up a simulation example.
# calulate variance of risk estimates:
Var_RV = RV*(1-RV)/NV
Var_RU = RU*(1-RU)/NU
# set-up MC draws:
B = 10000
RVs = RV + np.random.normal(0, 1, B)*(Var_RV)**.5
RUs = RU + np.random.normal(0, 1, B)*(Var_RU)**.5
VEs= (RUs - RVs)/RUs
CI_VE_L = np.quantile(VEs, .025)
CI_VE_U = np.quantile(VEs, .975)
print("95 % confidence interval is [" + str(CI_VE_L), ",",
str(CI_VE_U), "]" )
CI_VE_L = np.quantile(VEs, .05)
print("95 % confidence interval is [" + str(CI_VE_L), ",",
str(1), "]" )
from sklearn.neighbors import KernelDensity
import matplotlib
import matplotlib.pyplot as plt
from scipy.stats import norm
from sklearn.neighbors import KernelDensity
from sklearn.utils.fixes import parse_version
# instantiate and fit the KDE model
X= VEs[:, np.newaxis]
X_plot = np.linspace(0, 1, 1000)[:, np.newaxis]
kde = KernelDensity(kernel='gaussian', bandwidth=0.02).fit(X)
log_dens = kde.score_samples(X_plot)
plt.fill_between(X_plot[:, 0], np.exp(log_dens))
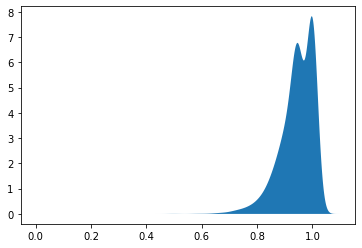
Overall VE is 0.9470690822010516
95 % confidence interval is [0.8112216059928701 , 1.0540078413340088 ]
95 % confidence interval is [0.8389839327867682 , 1 ]
<matplotlib.collections.PolyCollection at 0x7f12db008f90>

NV = 3239+805;
NU = 3255+812;
RV = 1/NV;
RU = (14+5)/NU;
VE = (RU - RV)/RU;
print("Overall VE is "+ str(VE))
B = 10000 #number of simulation draw
#numpy.random.binomial(n, p, size=None)
RVs = np.random.binomial(NV, RV, B)
RUs = np.random.binomial(NU, RU, B)
VEs= (RUs - RVs)/RUs
CI_VE_L = np.quantile(VEs, .025)
CI_VE_U = np.quantile(VEs, .975)
print("95 % confidence interval is [" + str(CI_VE_L), ",",
str(CI_VE_U), "]" )
CI_VE_L = np.quantile(VEs, .05)
print("95 % confidence interval is [" + str(CI_VE_L), ",",
str(1), "]" )
from sklearn.neighbors import KernelDensity
import matplotlib
import matplotlib.pyplot as plt
from scipy.stats import norm
from sklearn.neighbors import KernelDensity
from sklearn.utils.fixes import parse_version
# instantiate and fit the KDE model
X= VEs[:, np.newaxis]
X_plot = np.linspace(0, 1.1, 1000)[:, np.newaxis]
kde = KernelDensity(kernel='gaussian', bandwidth=0.02).fit(X)
log_dens = kde.score_samples(X_plot)
plt.fill_between(X_plot[:, 0], np.exp(log_dens))
Overall VE is 0.9470690822010516
95 % confidence interval is [0.8 , 1.0 ]
95 % confidence interval is [0.8333333333333334 , 1 ]
<matplotlib.collections.PolyCollection at 0x7f12db014050>
4.3. Exact Binomial Test Inversion#
It is possible to use exact inference by inverting tests based on the exact binomial nature of the outcome variable. Here, we perform the Cornfield Procedure to find the exact confidence interval on the estimate of vaccine efficacy.
def CI_journal(NV, RV_infected, NU, RU_infected):
# from https://www.medrxiv.org/content/10.1101/2020.12.16.20248359v1.full.pdf
RV = RV_infected/NV;
RU = RU_infected/NU;
RR = RV/RU;
print("Overall Risk Ratio is "+ str(RR))
# this recovers the number in the table.
# we set up a simulation example.
# calulate variance of risk estimates:
stat = 1.96*(1/RV_infected + 1/RU_infected)**.5
print("95 % confidence interval is [" + str(1-RR*np.exp(stat)), ",",
str(1-RR*np.exp(-stat)), "]" )
# Exact CI exploiting Bernoulli outcome using the Cornfield Procedure
NV = 19965
NU = 20172
RV = 9/NV
RU = 169/NU
VE = (RU - RV)/RU
print(f"""
Overall VE is {VE}
""")
95 % confidence interval is [0.9066666666666666 , 0.9782608695652174 ]
Overall VE is 0.9461934124362605
95% confidence interval is [ 0.9139072847682119, 0.9139072847682119 ]
Note that this exactly recovers the result in the FDA table (first row).
Next we repeat the cornfield procedure to find the exact confidence interval on vaccine effectiveness for the two groups that are 65 or older. Here we see a big discrepancy between various asymptotic approaches and the exact finite-sample inference. This occurs because the binomial counts are too low for central limit theorems to work successfully.
# Exact CI exploiting Bernoulli outcome for the two groups that are 65 or older
NV = 3239+805
NU = 3255+812
RV = 1/NV
RU = (14+5)/NU
VE = (RU - RV)/RU
print(f"""
Overall VE is {VE}
""")
Overall VE is 0.9470690822010516
95% confidence interval is [ 0.8333333333333334, 0.8333333333333334 ]


