7. Linear Penalized Regs

7.1. Penalized Linear Regressions: A Simulation Experiment

7.2. Data Generating Process: Approximately Sparse

#Imoprt relevant packages
import random
random.seed(1)
import numpy as np
import math
import matplotlib.pyplot as plt
import warnings
import statsmodels.api as sm
warnings.filterwarnings('ignore')

n = 100
p = 400

Z = np.random.uniform( low = 0 , high = 1 , size = n) - 1/2 

W = ( np.random.uniform( low = 0 , high = 1 , size = n * p ) - 1/2 ).\
        reshape( n , p )

beta = ((1/ np.arange(1, p + 1 )) ** 2)

gX = np.exp( 4 * Z ) + (W @ beta)
gX

X = np.concatenate( ( Z.reshape(Z.size, 1), Z.reshape(Z.size, 1) \
                     ** 2, Z.reshape(Z.size, 1) ** 3, W ) , axis = 1 )

mean = 0
sd = 1
Y = gX + np.random.normal( mean , sd, n )

# We use package Glmnet to carry out predictions using cross-validated lasso, ridge, and elastic net
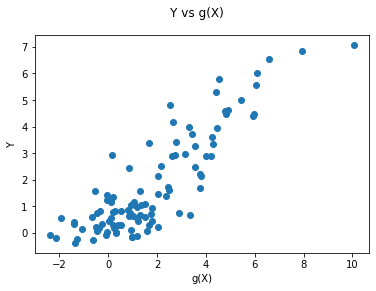
fig = plt.figure()
fig.suptitle('Y vs g(X)')
ax = fig.add_subplot(111)
plt.scatter( Y, gX)
plt.xlabel('g(X)')
plt.ylabel('Y')
plt.show()

print( f"theoretical R2:, {np.var(gX) / np.var( Y )}" ) 

np.var(gX) / np.var( Y ) #theoretical R-square in the simulation example

theoretical R2:, 0.6707376256265224

0.6707376256265224

We use package Glmnet to carry out predictions using cross-validated lasso, ridge, and elastic net

We should know that cv.glmnet function in r standarize X data by default. So, we have to standarize our data before the execution of sklearn package. The normalize parameter will help for this. However, the function cv.glamnet is also standarizing the Y variable and then unstadarize the coefficients from the regression. To do this with sklearn, we will standarize the Y variable before fitting with StandardScaler function. Finally, the r-function uses 10 folds by default so we will adjust our model to use cv=10 ten folds.

The parameter l1_ratio corresponds to alpha in the glmnet R package while alpha corresponds to the lambda parameter in glmnet. Specifically, l1_ratio = 1 is the lasso penalty. Currently, l1_ratio <= 0.01 is not reliable, unless you supply your own sequence of alpha.

from sklearn.linear_model import LassoCV
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import RidgeCV, ElasticNetCV

# Reshaping Y variable
Y_vec = Y.reshape( Y.size, 1)

# Scalar distribution
scaler = StandardScaler()
scaler.fit( Y_vec )
std_Y = scaler.transform( Y_vec )

# Regressions
fit_lasso_cv = LassoCV(cv = 10 , random_state = 0 , normalize = True ).fit( X, std_Y )
fit_ridge = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.0001 ).fit( X, std_Y )
fit_elnet = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.5, max_iter = 100000 ).fit( X, std_Y )

# Predictions
yhat_lasso_cv = scaler.inverse_transform( fit_lasso_cv.predict( X ).reshape(-1,1) )
yhat_ridge = scaler.inverse_transform( fit_ridge.predict( X ).reshape(-1,1) )
yhat_elnet = scaler.inverse_transform( fit_elnet.predict( X ).reshape(-1,1) )

MSE_lasso_cv = sm.OLS( ((gX.reshape(-1,1) - yhat_lasso_cv)**2 ) , np.ones( yhat_lasso_cv.shape )  ).fit().summary2().tables[1].round(3)
MSE_ridge = sm.OLS( ((gX.reshape(-1,1) - yhat_ridge)**2 ) , np.ones( yhat_ridge.size )  ).fit().summary2().tables[1].round(3)
MSE_elnet = sm.OLS( ((gX.reshape(-1,1) - yhat_elnet)**2 ) , np.ones( yhat_elnet.size )  ).fit().summary2().tables[1].round(3)
# our coefficient of MSE_elnet are far from r output

Here we compute the lasso and ols post lasso using plug-in choices for penalty levels, using package hdm

Rlasso functionality: it is searching the right set of regressors. This function was made for the case of p regressors and n observations where p >>>> n. It assumes that the error is i.i.d. The errors may be non-Gaussian or heteroscedastic.
The post lasso function makes OLS with the selected T regressors. To select those parameters, they use \(\lambda\) as variable to penalize
Funny thing: the function rlasso was named like that because it is the “rigorous” Lasso.
We find a Python code that tries to replicate the main function of hdm r-package. I was made by Max Huppertz. His library is this repository. Download its repository and copy this folder to your site-packages folder. In my case it is located here C:\Python\Python38\Lib\site-packages .

We need to install this package pip install multiprocess.

import hdmpy

fit_rlasso = hdmpy.rlasso(X, Y, post = False)
fit_rlasso_post = hdmpy.rlasso(X, Y, post = True)

yhat_rlasso = Y - fit_rlasso.est['residuals'].reshape( Y.size,  )
yhat_rlasso_post = Y - fit_rlasso_post.est['residuals'].reshape( Y.size ,  )

MSE_lasso = sm.OLS( ((gX - yhat_rlasso)**2 ) , np.ones( yhat_rlasso.size )  ).fit().summary2().tables[1].round(3)
MSE_lasso_post = sm.OLS( ((gX - yhat_rlasso_post)**2 ) , np.ones( yhat_rlasso_post.size )  ).fit().summary2().tables[1].round(3)

def lava_predict( x, y, iteration = 5 ):
    
    g1_rlasso = hdmpy.rlasso( x, y.reshape(-1,1) , post = False )
    g1 = y.reshape(-1,1) - g1_rlasso.est['residuals']

    new_dep_var = y.reshape(-1,1)-g1
    new_dep_var_vec = new_dep_var.reshape( new_dep_var.size, 1 )

    # Scalar distribution
    scaler = StandardScaler()
    scaler.fit( new_dep_var_vec )
    std_new_dep_var_vec = scaler.transform( new_dep_var_vec )

    fit_ridge_m1 = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.0001, alphas = np.array([20]) ).fit( x, std_new_dep_var_vec )
    m1 = scaler.inverse_transform( fit_ridge_m1.predict( x ).reshape(-1,1) )
    
    i = 1
    while i <= iteration:
        
        g1_rlasso = hdmpy.rlasso( x, y , post = False )
        g1 = y - g1_rlasso.est['residuals'].reshape( g1_rlasso.est['residuals'].size, )

        new_dep_var = y-g1
        new_dep_var_vec = new_dep_var.reshape( new_dep_var.size, 1 )

        # Scalar distribution
        scaler = StandardScaler()
        scaler.fit( new_dep_var_vec )
        std_new_dep_var_vec = scaler.transform( new_dep_var_vec )

        fit_ridge_m1 = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.0001, alphas = np.array([20]) ).fit( x, std_new_dep_var_vec )
        m1 = scaler.inverse_transform( fit_ridge_m1.predict( x ).reshape(-1,1) )
        
        i = i + 1
        
    return ( g1.reshape(-1,1) + m1.reshape(-1,1) )
        

Next we code up lava, which alternates the fitting of lasso and ridge

yhat_lava = lava_predict( X, Y )
MSE_lava = sm.OLS( ((gX.reshape(-1,1) - yhat_lava)**2 ) , np.ones( yhat_lava.size )  ).fit().summary2().tables[1].round(3)

import pandas as pd

table2 = np.zeros( (6, 2) )

table2[0, 0:] = MSE_lasso_cv.iloc[0, 0:2].to_list()
table2[1, 0:] = MSE_ridge.iloc[0, 0:2].to_list()
table2[2, 0:] = MSE_elnet.iloc[0, 0:2].to_list()
table2[3, 0:] = MSE_lasso.iloc[0, 0:2].to_list()
table2[4, 0:] = MSE_lasso_post.iloc[0, 0:2].to_list()
table2[5, 0:] = MSE_lava.iloc[0, 0:2].to_list()



table2_pandas = pd.DataFrame( table2, columns = [ "MSA","S.E. for MSA" ])
table2_pandas.index = [ "Cross-Validated Lasso",\
                       "Cross-Validated Ridge", "Cross-Validated elnet",\
                       "Lasso", "Post-Lasso", "Lava" ]
table2_pandas = table2_pandas.round(3)
table2_html = table2_pandas.to_html()
table2_pandas

	MSA	S.E. for MSA
Cross-Validated Lasso	0.159	0.021
Cross-Validated Ridge	3.032	0.441
Cross-Validated elnet	0.542	0.074
Lasso	0.223	0.036
Post-Lasso	0.276	0.033
Lava	0.223	0.036

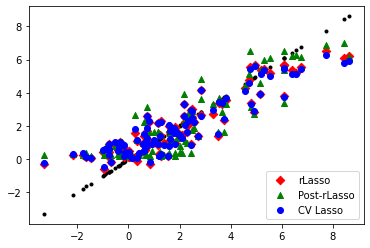
import matplotlib.pyplot as plt

fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.scatter( gX, gX , marker = '.', c = 'black' )
ax1.scatter( gX, yhat_rlasso , marker = 'D' , c = 'red' , label = 'rLasso' )
ax1.scatter( gX, yhat_rlasso_post , marker = '^' , c = 'green' , label = 'Post-rLasso')
ax1.scatter( gX, yhat_lasso_cv , marker = 'o' , c = 'blue' , label = 'CV Lasso')
plt.legend(loc='lower right')
plt.show()

7.3. Data Generating Process: Approximately Sparse + Small Dense Part

n = 100
p = 400

Z = np.random.uniform( low = 0 , high = 1 , size = n) - 1/2 

W = ( np.random.uniform( low = 0 , high = 1 , size = n * p ) - 1/2 ).\
        reshape( n , p )
mean = 0
sd = 1

beta = ((np.random.normal( mean , sd, p )) * 0.2)
gX = np.exp( 4 * Z ) + (W @ beta)
X = np.concatenate( ( Z.reshape(Z.size, 1), Z.reshape(Z.size, 1) \
                     ** 2, Z.reshape(Z.size, 1) ** 3, W ) , axis = 1 )
random.seed(2)
Y = gX + np.random.normal( mean , sd, n )

# We use package Glmnet to carry out predictions using cross-validated lasso, ridge, and elastic net
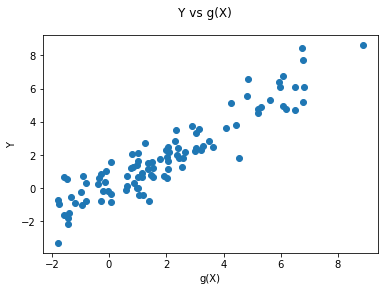
fig = plt.figure()
fig.suptitle('Y vs g(X)')
ax = fig.add_subplot(111)
plt.scatter( Y, gX)
plt.xlabel('g(X)')
plt.ylabel('Y')
plt.show()

print( f"theoretical R2:, {np.var(gX) / np.var( Y )}" ) 

np.var(gX) / np.var( Y ) #theoretical R-square in the simulation example

theoretical R2:, 0.9504535223829087

0.9504535223829087

# Reshaping Y variable
Y_vec = Y.reshape( Y.size, 1)

# Scalar distribution
scaler = StandardScaler()
scaler.fit( Y_vec )
std_Y = scaler.transform( Y_vec )

# Regressions
fit_lasso_cv = LassoCV(cv = 10 , random_state = 0 , normalize = True ).fit( X, std_Y )
fit_ridge = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.0001 ).fit( X, std_Y )
fit_elnet = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.5, max_iter = 100000 ).fit( X, std_Y )

# Predictions
yhat_lasso_cv = scaler.inverse_transform( fit_lasso_cv.predict( X ).reshape(-1,1) )
yhat_ridge = scaler.inverse_transform( fit_ridge.predict( X ).reshape(-1,1) )
yhat_elnet = scaler.inverse_transform( fit_elnet.predict( X ).reshape(-1,1) )

import statsmodels.api as sm

MSE_lasso_cv = sm.OLS( ((gX.reshape(-1,1) - yhat_lasso_cv)**2 ) , np.ones( yhat_lasso_cv.shape )  ).fit().summary2().tables[1].round(3)
MSE_ridge = sm.OLS( ((gX.reshape(-1,1) - yhat_ridge)**2 ) , np.ones( yhat_ridge.size )  ).fit().summary2().tables[1].round(3)
MSE_elnet = sm.OLS( ((gX.reshape(-1,1) - yhat_elnet)**2 ) , np.ones( yhat_elnet.size )  ).fit().summary2().tables[1].round(3)
# our coefficient of MSE_elnet are far from r output

fit_rlasso = hdmpy.rlasso(X, Y, post = False)
fit_rlasso_post = hdmpy.rlasso(X, Y, post = True)

yhat_rlasso = Y - fit_rlasso.est['residuals'].reshape( Y.size,  )
yhat_rlasso_post = Y - fit_rlasso_post.est['residuals'].reshape( Y.size ,  )

MSE_lasso = sm.OLS( ((gX - yhat_rlasso)**2 ) , np.ones( yhat_rlasso.size )  ).fit().summary2().tables[1].round(3)
MSE_lasso_post = sm.OLS( ((gX - yhat_rlasso_post)**2 ) , np.ones( yhat_rlasso_post.size )  ).fit().summary2().tables[1].round(3)

def lava_predict( x, y, iteration = 5 ):
    
    g1_rlasso = hdmpy.rlasso( x, y.reshape(-1,1) , post = False )
    g1 = y.reshape(-1,1) - g1_rlasso.est['residuals']

    new_dep_var = y.reshape(-1,1)-g1
    new_dep_var_vec = new_dep_var.reshape( new_dep_var.size, 1 )

    # Scalar distribution
    scaler = StandardScaler()
    scaler.fit( new_dep_var_vec )
    std_new_dep_var_vec = scaler.transform( new_dep_var_vec )

    fit_ridge_m1 = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.0001, alphas = np.array([20]) ).fit( x, std_new_dep_var_vec )
    m1 = scaler.inverse_transform( fit_ridge_m1.predict( x ).reshape(-1,1) )
    
    i = 1
    while i <= iteration:
        
        g1_rlasso = hdmpy.rlasso( x, y , post = False )
        g1 = y - g1_rlasso.est['residuals'].reshape( g1_rlasso.est['residuals'].size, )

        new_dep_var = y-g1
        new_dep_var_vec = new_dep_var.reshape( new_dep_var.size, 1 )

        # Scalar distribution
        scaler = StandardScaler()
        scaler.fit( new_dep_var_vec )
        std_new_dep_var_vec = scaler.transform( new_dep_var_vec )

        fit_ridge_m1 = ElasticNetCV( cv = 10 , normalize = True , random_state = 0 , l1_ratio = 0.0001, alphas = np.array([20]) ).fit( x, std_new_dep_var_vec )
        m1 = scaler.inverse_transform( fit_ridge_m1.predict( x ).reshape(-1,1) )
        
        i = i + 1
        
    return ( g1.reshape(-1,1) + m1.reshape(-1,1) )
        

yhat_lava = lava_predict( X, Y )
MSE_lava = sm.OLS( ((gX.reshape(-1,1) - yhat_lava)**2 ) , np.ones( yhat_lava.size )  ).fit().summary2().tables[1].round(3)

table2 = np.zeros( (6, 2) )

table2[0, 0:] = MSE_lasso_cv.iloc[0, 0:2].to_list()
table2[1, 0:] = MSE_ridge.iloc[0, 0:2].to_list()
table2[2, 0:] = MSE_elnet.iloc[0, 0:2].to_list()
table2[3, 0:] = MSE_lasso.iloc[0, 0:2].to_list()
table2[4, 0:] = MSE_lasso_post.iloc[0, 0:2].to_list()
table2[5, 0:] = MSE_lava.iloc[0, 0:2].to_list()



table2_pandas = pd.DataFrame( table2, columns = [ "MSA","S.E. for MSA" ])
table2_pandas.index = [ "Cross-Validated Lasso",\
                       "Cross-Validated Ridge", "Cross-Validated elnet",\
                       "Lasso", "Post-Lasso", "Lava" ]
table2_pandas = table2_pandas.round(3)
table2_html = table2_pandas.to_html()
table2_pandas

	MSA	S.E. for MSA
Cross-Validated Lasso	1.218	0.172
Cross-Validated Ridge	4.979	0.723
Cross-Validated elnet	1.019	0.156
Lasso	1.113	0.157
Post-Lasso	1.468	0.200
Lava	1.110	0.157

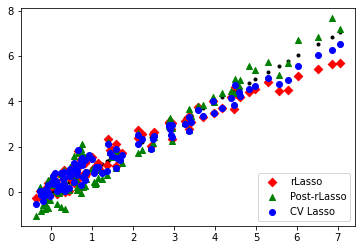
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.scatter( gX, gX , marker = '.', c = 'black' )
ax1.scatter( gX, yhat_rlasso , marker = 'D' , c = 'red' , label = 'rLasso' )
ax1.scatter( gX, yhat_rlasso_post , marker = '^' , c = 'green' , label = 'Post-rLasso')
ax1.scatter( gX, yhat_lasso_cv , marker = 'o' , c = 'blue' , label = 'CV Lasso')
plt.legend(loc='lower right')
plt.show()