24. Debiased ML for Partially Linear IV Model in Python#

24.1. Double/Debiased ML for Partially Linear IV Model#

References:

https://arxiv.org/abs/1608.00060

https://www.amazon.com/Business-Data-Science-Combining-Accelerate/dp/1260452778

The code is based on the book.

24.2. Partially Linear IV Model#

We consider the partially linear structural equation model:

\[\begin{split} \begin{align}\tag{1} & Y - D\theta_0 = g_0(X) + \zeta, & E[\zeta \mid Z,X]= 0,\\ \end{align} \end{split}\]
\[ \begin{align}\tag{2} & Z = m_0(X) + V, & E[V \mid X] = 0. \end{align} \]

Note that this model is not a regression model unless \(Z=D\). The model is a canonical model in causal inference, going back to P. Wright’s work on IV methods for estimaing demand/supply equations, with the modern difference being that \(g_0\) and \(m_0\) are nonlinear, potentially complicated functions of high-dimensional \(X\).

The idea of this model is that there is a structural or causal relation between \(Y\) and \(D\), captured by \(\theta_0\), and \(g_0(X) + \zeta\) is the stochastic error, partly explained by covariates \(X\). \(V\) and \(\zeta\) are stochastic errors that are not explained by \(X\). Since \(Y\) and \(D\) are jointly determined, we need an external factor, commonly referred to as an instrument, \(Z\) to create exogenous variation in \(D\). Note that \(Z\) should affect \(D\). The \(X\) here serve again as confounding factors, so we can think of variation in \(Z\) as being exogenous only conditional on \(X\).

The causal DAG this model corresponds to is given by:

\[ \begin{align} Z \to D, X \to (Y, Z, D), L \to (Y,D), \end{align} \]

where \(L\) is the latent confounder affecting both \(Y\) and \(D\), but not \(Z\).

Example

A simple contextual example is from biostatistics, where \(Y\) is a health outcome and \(D\) is indicator of smoking. Thus, \(\theta_0\) is captures the effect of smoking on health. Health outcome \(Y\) and smoking behavior \(D\) are treated as being jointly determined. \(X\) represents patient characteristics, and \(Z\) could be a doctor’s advice not to smoke (or another behavioral treatment) that may affect the outcome \(Y\) only through shifting the behavior \(D\), conditional on characteristics \(X\).

PLIVM in Residualized Form

The PLIV model above can be rewritten in the following residualized form:

\[ \begin{align} \tilde Y = \tilde D \theta_0 + \zeta, \quad E[\zeta \mid V,X]= 0, \end{align} \]

where

\[\begin{split} \begin{align} \tilde Y = (Y- \ell_0(X)), \quad \ell_0(X) = E[Y \mid X] \\ \tilde D = (D - r_0(X)), \quad r_0(X) = E[D \mid X] \\ \tilde Z = (Z- m_0(X)), \quad m_0(X) = E[Z \mid X]. \end{align} \end{split}\]

The tilded variables above represent original variables after taking out or “partialling out” the effect of \(X\). Note that \(\theta_0\) is identified from this equation if \(V\) and \(U\) have non-zero correlation, which automatically means that \(U\) and \(V\) must have non-zero variation.

DML for PLIV Model

Given identification, DML proceeds as follows

Compute the estimates \(\hat \ell_0\), \(\hat r_0\), and \(\hat m_0\) , which amounts to solving the three problems of predicting \(Y\), \(D\), and \(Z\) using \(X\), using any generic ML method, giving us estimated residuals

\[\begin{split} \begin{align} \tilde Y = Y - \hat \ell_0(X), \\ \tilde D= D - \hat r_0(X), \\ \tilde Z = Z- \hat m_0(X). \end{align} \end{split}\]

The estimates should be of a cross-validated form, as detailed in the algorithm below.

Estimate \(\theta_0\) by the the intstrumental variable regression of \(\tilde Y\) on \(\tilde D\) using \(\tilde Z\) as an instrument. Use the conventional inference for the IV regression estimator, ignoring the estimation error in these residuals.

The reason we work with this residualized form is that it eliminates the bias arising when solving the prediction problem in stage 1. The role of cross-validation is to avoid another source of bias due to potential overfitting.

The estimator is adaptive, in the sense that the first stage estimation errors do not affect the second stage errors.

# Import packages
import pandas as pd
import numpy as np
import pyreadr
import os
from urllib.request import urlopen
from sklearn import preprocessing
import patsy

from numpy import loadtxt
from keras.models import Sequential
from keras.layers import Dense

import hdmpy
import numpy as np
import random
import statsmodels.api as sm
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.linear_model import LassoCV
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import RidgeCV, ElasticNetCV
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
import itertools
from pandas.api.types import is_string_dtype
from pandas.api.types import is_numeric_dtype
from pandas.api.types import is_categorical_dtype
from itertools import compress
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.feature_selection import SelectFromModel
from statsmodels.tools import add_constant
from sklearn.linear_model import ElasticNet
import hdmpy
from scipy.stats import chi2
from sklearn.model_selection import KFold
import warnings
warnings.filterwarnings('ignore')

from linearmodels.iv import IV2SLS

import numpy as np
from statsmodels.api import add_constant
from linearmodels.datasets import mroz

link="https://raw.githubusercontent.com/d2cml-ai/14.388_py/main/data/ajr.RData"
response = urlopen(link)
content = response.read()
fhandle = open( 'ajr.Rdata', 'wb')
fhandle.write(content)
fhandle.close()
result = pyreadr.read_r("ajr.Rdata")
os.remove("ajr.Rdata")

# Extracting the data frame from rdata_read
AJR = result[ 'AJR' ]
AJR.shape

(64, 11)

def DML2_for_PLIVM(x, d, z , y, dreg, yreg, zreg, nfold = 2 ):
    
    kf = KFold(n_splits = nfold, shuffle=True) #Here we use kfold to generate kfolds
    I = np.arange(0, len(d)) #To have a id vector from data
    train_id, test_id =  [], [] #arrays to store kfold's ids

    #generate and store kfold's id
    for kfold_index in kf.split(I):
        train_id.append(kfold_index[0])
        test_id.append(kfold_index[1])
    
    # Create array to save errors 
    dtil = np.zeros( len(z) ).reshape( len(z) , 1 )
    ytil = np.zeros( len(z) ).reshape( len(z) , 1 )
    ztil = np.zeros( len(z) ).reshape( len(z) , 1 )
    
    total_modelos = []
    
    total_sample = 0
    # loop to save results
    for b in range(0,len(train_id)):

        # Lasso regression, excluding folds selected 
        dfit = dreg(x[train_id[b],], d[train_id[b],])
        zfit = zreg(x[train_id[b],], z[train_id[b],])
        yfit = yreg(x[train_id[b],], y[train_id[b],])

        # predict estimates using the 
        dhat = dfit.predict( x[test_id[b],] )
        zhat = zfit.predict( x[test_id[b],] )
        yhat = yfit.predict( x[test_id[b],] )
        
        # save errors  
        dtil[test_id[b]] = d[test_id[b],] - dhat.reshape( -1 , 1 )
        ztil[test_id[b]] = z[test_id[b],] - zhat.reshape( -1 , 1 )
        ytil[test_id[b]] = y[test_id[b],] - yhat.reshape( -1 , 1 )
        
        total_modelos.append( dfit )
        
        print(b, " ")
    
    # Create dataframe
    ivfit = IV2SLS( exog = None , endog = dtil , dependent = ytil , instruments = ztil ).fit( cov_type = 'unadjusted' ) ## unadjusted == homocedastick
   
    # OLS clustering at the County level
    coef_est =  ivfit.params[0]
    se = ivfit.std_errors[0]
    print( f"\n Coefficient (se) = {coef_est} ({se})" )
    Final_result = { 'coef_est' : coef_est , 'se' : se , 'dtil' : dtil , 'ytil' : ytil , 'ztil' : ztil , 'modelos' : total_modelos }
       
    return Final_result

24.3. Emprical Example: Acemoglu, Jonsohn, Robinson (AER).#

  • Y is log GDP;

  • D is a measure of Protection from Expropriation, a proxy for quality of insitutions;

  • Z is the log of Settler’s mortality;

  • W are geographical variables (latitude, latitude squared, continent dummies as well as interactions)

y = AJR[['GDP']].to_numpy()

d = AJR[['Exprop']].to_numpy()

z = AJR[['logMort']].to_numpy()

xraw_formula =  " GDP ~ Latitude+ Africa+Asia + Namer + Samer"
x_formula = " GDP ~ -1 + ( Latitude + Latitude2 + Africa + Asia + Namer + Samer ) ** 2"

y_model, xraw_dframe = patsy.dmatrices( xraw_formula, AJR , return_type='matrix')
y_model, x_dframe = patsy.dmatrices( x_formula, AJR , return_type='matrix')

xraw = np.asarray( xraw_dframe , dtype = np.float64 )
x = np.asarray( x_dframe , dtype = np.float64)

Information from random Forest link1, link2

y_model, x_dframe2 = patsy.dmatrices( x_formula, AJR , return_type='dataframe')

x_dframe2
Latitude Latitude2 Africa Asia Namer Samer Latitude:Latitude2 Latitude:Africa Latitude:Asia Latitude:Namer ... Latitude2:Africa Latitude2:Asia Latitude2:Namer Latitude2:Samer Africa:Asia Africa:Namer Africa:Samer Asia:Namer Asia:Samer Namer:Samer
0 0.3111 0.096783 1.0 0.0 0.0 0.0 0.030109 0.3111 0.0000 0.0000 ... 0.096783 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.0 0.0 0.0
1 0.1367 0.018687 1.0 0.0 0.0 0.0 0.002554 0.1367 0.0000 0.0000 ... 0.018687 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.0 0.0 0.0
2 0.3778 0.142733 0.0 0.0 0.0 1.0 0.053924 0.0000 0.0000 0.0000 ... 0.000000 0.000000 0.000000 0.142733 0.0 0.0 0.0 0.0 0.0 0.0
3 0.3000 0.090000 0.0 0.0 0.0 0.0 0.027000 0.0000 0.0000 0.0000 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.0 0.0 0.0
4 0.2683 0.071985 0.0 0.0 1.0 0.0 0.019314 0.0000 0.0000 0.2683 ... 0.000000 0.000000 0.071985 0.000000 0.0 0.0 0.0 0.0 0.0 0.0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
59 0.3667 0.134469 0.0 0.0 0.0 1.0 0.049310 0.0000 0.0000 0.0000 ... 0.000000 0.000000 0.000000 0.134469 0.0 0.0 0.0 0.0 0.0 0.0
60 0.4222 0.178253 0.0 0.0 1.0 0.0 0.075258 0.0000 0.0000 0.4222 ... 0.000000 0.000000 0.178253 0.000000 0.0 0.0 0.0 0.0 0.0 0.0
61 0.0889 0.007903 0.0 0.0 0.0 1.0 0.000703 0.0000 0.0000 0.0000 ... 0.000000 0.000000 0.000000 0.007903 0.0 0.0 0.0 0.0 0.0 0.0
62 0.1778 0.031613 0.0 1.0 0.0 0.0 0.005621 0.0000 0.1778 0.0000 ... 0.000000 0.031613 0.000000 0.000000 0.0 0.0 0.0 0.0 0.0 0.0
63 0.0000 0.000000 1.0 0.0 0.0 0.0 0.000000 0.0000 0.0000 0.0000 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.0 0.0 0.0

64 rows × 21 columns

def dreg( x_1 , d_1 ):
    
    if d_1 is not None and ( d_1.dtype != str ):
        mtry1 = max( [ np.round( ( x_1.shape[ 1 ]/3 ) ) , 1 ] ).astype(int)
    else:
        mtry1 = np.round( np.sqrt( x_1.shape[ 1 ] ) ).astype(int)

    if d_1 is not None and ( d_1.dtype != str ):
        nodesize1 = 5
    else:
        nodesize1 = 1
    
    result = RandomForestRegressor( random_state = 0 , n_estimators = 500 , max_features = mtry1 , n_jobs = 4 , min_samples_leaf = nodesize1 ).fit( x_1 , d_1 )
    return result

def yreg( x_1 , y_1 ):
    if y_1 is not None and ( y_1.dtype != str ):
        mtry1 = max( [ np.round( ( x_1.shape[ 1 ]/3 ) ) , 1 ] ).astype(int)
    else:
        mtry1 = np.round( np.sqrt( x_1.shape[ 1 ] ) ).astype(int)

    if y_1 is not None and ( y_1.dtype != str ):
        nodesize1 = 5
    else:
        nodesize1 = 1
        
    result = RandomForestRegressor( random_state = 0 , n_estimators = 500 , max_features = mtry1 , n_jobs = 4 , min_samples_leaf = nodesize1 ).fit( x_1, y_1 )
    return result

def zreg( x_1 , z_1 ):
    
    if z_1 is not None and ( z_1.dtype != str ):
        mtry1 = max( [ np.round( ( x_1.shape[ 1 ]/3 ) ) , 1 ] ).astype(int)
    else:
        mtry1 = np.round( np.sqrt( x_1.shape[ 1 ] ) ).astype(int)

    if z_1 is not None and ( z_1.dtype != str ):
        nodesize1 = 5
    else:
        nodesize1 = 1
        
    result = RandomForestRegressor( random_state = 0 , n_estimators = 500 , max_features = mtry1 , n_jobs = 4 , min_samples_leaf = nodesize1 ).fit( x_1, z_1 )
    return result

print( "\n DML with Post-Lasso \n" )

 DML with Post-Lasso 

DML2_RF = DML2_for_PLIVM(xraw, d, z, y, dreg, yreg, zreg, nfold=20)

0  
1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  

 Coefficient (se) = 0.8113768412168717 (0.25866023849580644)

class rlasso_sklearn:
    
    def __init__(self, post ):
        self.post = post
       
    def fit( self, X, Y ):
        
        self.X = X
        self.Y = Y
        
        # Standarization of X and Y
        self.rlasso_model = hdmpy.rlasso( X , Y , post = self.post )                
        return self
    
    def predict( self , X_1 ):
        self.X_1 = X_1
        beta = self.rlasso_model.est['coefficients'].to_numpy()
        
        if beta.sum() == 0:
            prediction = np.repeat( self.rlasso_model.est['intercept'] , self.X_1.shape[0] )
        
        else:
            prediction = ( add_constant( self.X_1 , has_constant = 'add') @ beta ).flatten()
                
        return prediction

# DML with PostLasso
print( "\n DML with Lasso \n" )
def dreg(x, d):
    result = rlasso_sklearn( post = True ).fit( x , d )
    return result

def yreg(x,y):
    result = rlasso_sklearn( post = True ).fit( x , y )
    return result

def zreg(x,z):
    result = rlasso_sklearn( post = True ).fit( x , z )
    return result

 DML with Lasso 

DML2_lasso = DML2_for_PLIVM(x, d, z, y, dreg, yreg, zreg, nfold = 20 )

0  
1  
2  
3  
4  
5  
6  
7  
8  
9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  

 Coefficient (se) = 0.7092468711866841 (0.1611789001019162)

# Compare Forest vs Lasso
comp_tab_numpy = np.zeros( ( 3 , 2 ) )

comp_tab_numpy[ 0 , : ] = [ np.sqrt( np.mean( DML2_RF['ytil'] ** 2 ) ) , np.sqrt( np.mean( DML2_lasso['ytil'] ** 2 ) ) ]
comp_tab_numpy[ 1 , : ] = [ np.sqrt( np.mean( DML2_RF['dtil'] ** 2 ) ) , np.sqrt( np.mean( DML2_lasso['dtil'] ** 2 ) ) ]
comp_tab_numpy[ 2 , : ] = [ np.sqrt( np.mean( DML2_RF['ztil'] ** 2 ) ) , np.sqrt( np.mean( DML2_lasso['ztil'] ** 2 ) ) ]

comp_tab = pd.DataFrame( comp_tab_numpy , columns = [ 'RF' ,'LASSO' ] , index = [ "RMSE for Y:", "RMSE for D:", "RMSE for Z:" ] )

comp_tab
RF LASSO
RMSE for Y: 0.798088 0.928451
RMSE for D: 1.326933 1.595742
RMSE for Z: 0.946177 1.053832

24.4. Examine if we have weak instruments#

sm.OLS( DML2_lasso[ 'dtil' ] , DML2_lasso[ 'ztil' ] ).fit( cov_type = 'HC1', use_t = True ).summary()
OLS Regression Results
Dep. Variable: y R-squared (uncentered): 0.173
Model: OLS Adj. R-squared (uncentered): 0.160
Method: Least Squares F-statistic: 9.184
Date: Tue, 26 Jul 2022 Prob (F-statistic): 0.00354
Time: 00:33:58 Log-Likelihood: -114.65
No. Observations: 64 AIC: 231.3
Df Residuals: 63 BIC: 233.5
Df Model: 1
Covariance Type: HC1
coef std err t P>|t| [0.025 0.975]
x1 -0.6295 0.208 -3.031 0.004 -1.045 -0.214
Omnibus: 1.025 Durbin-Watson: 1.701
Prob(Omnibus): 0.599 Jarque-Bera (JB): 0.926
Skew: -0.047 Prob(JB): 0.630
Kurtosis: 2.418 Cond. No. 1.00


Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors are heteroscedasticity robust (HC1)
sm.OLS( DML2_RF[ 'dtil' ] , DML2_RF[ 'ztil' ] ).fit( cov_type = 'HC1', use_t = True ).summary()
OLS Regression Results
Dep. Variable: y R-squared (uncentered): 0.087
Model: OLS Adj. R-squared (uncentered): 0.073
Method: Least Squares F-statistic: 4.537
Date: Tue, 26 Jul 2022 Prob (F-statistic): 0.0371
Time: 00:34:00 Log-Likelihood: -105.99
No. Observations: 64 AIC: 214.0
Df Residuals: 63 BIC: 216.1
Df Model: 1
Covariance Type: HC1
coef std err t P>|t| [0.025 0.975]
x1 -0.4146 0.195 -2.130 0.037 -0.804 -0.026
Omnibus: 0.476 Durbin-Watson: 1.615
Prob(Omnibus): 0.788 Jarque-Bera (JB): 0.375
Skew: 0.183 Prob(JB): 0.829
Kurtosis: 2.919 Cond. No. 1.00


Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors are heteroscedasticity robust (HC1)

24.5. We do have weak instruments, because t-stats in regression \(\tilde D \sim \tilde Z\) are less than 4 in absolute value#

So let’s carry out DML inference combined with Anderson-Rubin Idea

# DML-AR (DML with Anderson-Rubin) 
def DML_AR_PLIV( rY, rD, rZ, grid, alpha = 0.05 ):
    n = rY.size
    Cstat = np.zeros( grid.size )

    for i in range( 0 , grid.size ):
        Cstat[ i ] = n * ( ( np.mean( ( rY - grid[ i ] * rD ) * rZ )  ) ** 2 ) / np.var( ( rY - grid[ i ] * rD ) * rZ )

    LB = np.min( grid[  Cstat < chi2.ppf( 1 - alpha , 1) ] )
    UB = np.max( grid[  Cstat < chi2.ppf( 1 - alpha , 1) ] )
    
    print( "UB =" , UB, "LB ="  ,LB)
    fig, ax = plt.subplots(figsize=(12, 6))

    ax.plot(grid, Cstat, color='black', label='Sine wave' )

    ax.axhline( y = chi2.ppf( 1 - 0.05 , 1) , linestyle = "--" )
    ax.axvline( x = LB , color = 'red' , linestyle = "--" )
    ax.axvline( x = UB , color = 'red' , linestyle = "--" )
    
    ax.set_ylabel('Statistic')
    ax.set_xlabel('Effect of institutions')

    plt.show()
    final_result = { 'UB' : UB , 'LB' : LB }
    
    return final_result

DML_AR_PLIV(rY = DML2_lasso['ytil'], rD= DML2_lasso['dtil'], rZ= DML2_lasso['ztil'],
           grid = np.arange( -2, 2.001, 0.01 ) )

UB = 1.7200000000000033 LB = 0.44000000000000217
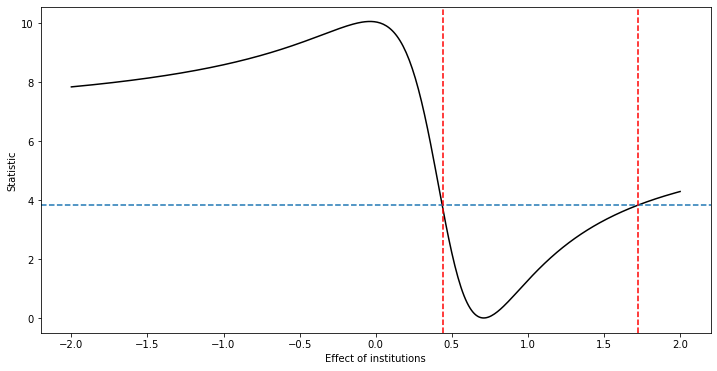
../_images/6323d0017fb87e892817a6dd9d2994a4a3eed150da55182466370e29de9b3798.png 
{'UB': 1.7200000000000033, 'LB': 0.44000000000000217}

DML_AR_PLIV(rY = DML2_RF['ytil'], rD= DML2_RF['dtil'], rZ= DML2_RF['ztil'],
           grid = np.arange( -2, 2.001, 0.01 ) )

UB = 2.0000000000000036 LB = 0.40000000000000213
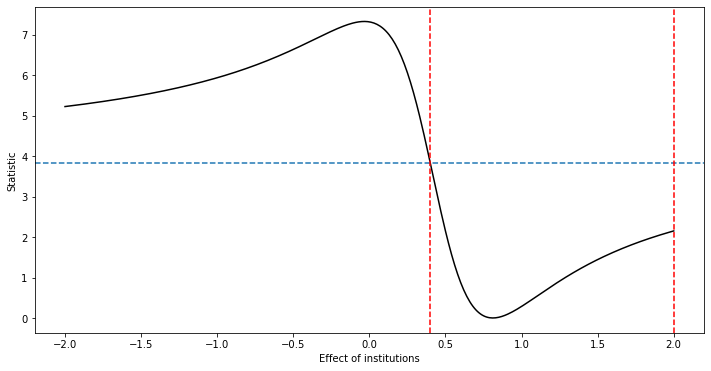
../_images/56180c0bbc4c75e150542a2065e1210fa0150f506730345447b2c1107bb116e2.png 
{'UB': 2.0000000000000036, 'LB': 0.40000000000000213}