21. Identification Analysis of 401(k) Example w DAGs#
Using Dagitty in the Analysis of Impact of 401(k) on Net Financial Wealth
#install and load packages
import graphviz as gv
from matplotlib import style
style.use("fivethirtyeight")
from statsmodels.iolib.summary2 import summary_col
import matplotlib.pyplot as plt
import networkx as nx
from optimaladj.CausalGraph import CausalGraph
Graphs for 401(K) Analsyis
Here we have
\(Y\) – net financial assets;
\(X\) – worker characteristics (income, family size, other retirement plans; see lecture notes for details);
\(F\) – latent (unobserved) firm characteristics
\(D\) – 401(K) eligibility, deterimined by \(F\) and \(X\)
21.1. State one graph (where F determines X) and plot it#
G1 = CausalGraph()
G1.add_node('Y', latent=False, pos=(4,0))
G1.add_node('D', latent=False, pos=(0,0))
G1.add_node('X', latent=False, pos=(2,-2))
G1.add_node("F", latent=True, pos=(0,-1))
pos=nx.get_node_attributes(G1,'pos')
G1.add_edge("D", "Y")
G1.add_edge("X", "D")
G1.add_edge("F", "X")
G1.add_edge("F", "D")
G1.add_edge("X", "Y")
nx.draw(G1, pos, with_labels = True, style = 'solid',
edge_color=['red' if G1.nodes[e[0]]['latent'] else 'gray' for e in G1.edges],
font_weight='bold', font_size=15, font_color='black',
node_color='white', arrowsize=30)
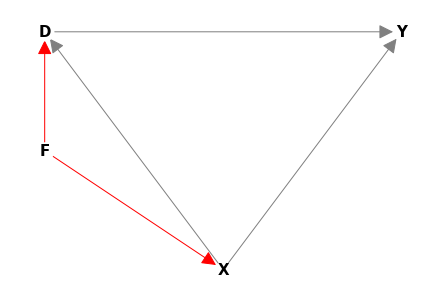
List minimal adjustment sets to identify causal effecs \(D \to Y\)
G1.optimal_minimal_adj_set("D", "Y", [], ["X"])
{'X'}
What is the underlying principle?
Here condition on X blocks backdoor paths from Y to D (Pearl). Dagitty correctly finds X (and does many more correct decisions, when we consider more elaborate structures. Why do we want to consider more elaborate structures? The very empirical problem requires us to do so!
21.2. Another Graph (wherere \(X\) determine \(F\)):#
G2 = CausalGraph()
G2.add_node('Y', latent=False, pos=(4,0))
G2.add_node('D', latent=False, pos=(0,0))
G2.add_node('X', latent=False, pos=(2,-2))
G2.add_node("F", latent=True, pos=(0,-1))
pos=nx.get_node_attributes(G2,'pos')
G2.add_edge("D", "Y")
G2.add_edge("X", "D")
G2.add_edge("X", "F")
G2.add_edge("F", "D")
G2.add_edge("X", "Y")
nx.draw(G2, pos, with_labels = True, style = 'solid',
edge_color=['red' if G2.nodes[e[0]]['latent'] else 'gray' for e in G2.edges],
font_weight='bold', font_size=15, font_color='black',
node_color='white', arrowsize=30)
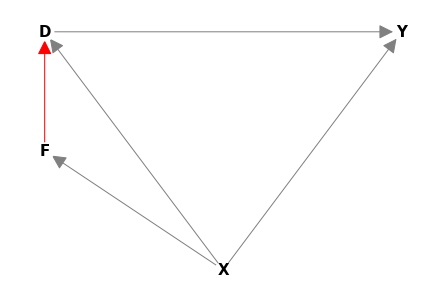
G2.optimal_minimal_adj_set("D", "Y", [], ["X"])
{'X'}
21.3. One more graph (encompassing previous ones), where (F, X) are jointly determined by latent factors \(A\). We can allow in fact the whole triple (D, F, X) to be jointly determined by latent factors \(A\).#
This is much more realistic graph to consider.
G3 = CausalGraph()
G3.add_node('Y', latent=False, pos=(4,0))
G3.add_node('D', latent=False, pos=(0,0))
G3.add_node('X', latent=False, pos=(2,-2))
G3.add_node("F", latent=True, pos=(0,-1))
G3.add_node("A", latent=True, pos=(-1,-1))
pos=nx.get_node_attributes(G3,'pos')
G3.add_edge("D", "Y")
G3.add_edge("X", "D")
G3.add_edge("F", "D")
G3.add_edge("A", "F")
G3.add_edge("A", "X")
G3.add_edge("A", "D")
G3.add_edge("X", "Y")
print(G3.optimal_minimal_adj_set("D", "Y", [], ["X"]))
nx.draw(G3, pos, with_labels = True, style = 'solid',
edge_color=['red' if G3.nodes[e[0]]['latent'] else 'gray' for e in G3.edges],
font_weight='bold', font_size=15, font_color='black',
node_color='white', arrowsize=30)
{'X'}
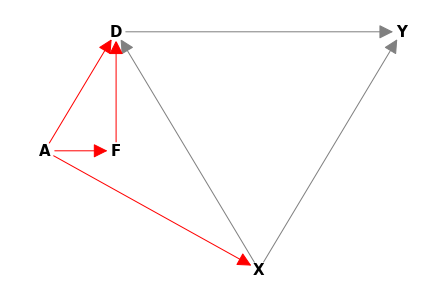
21.4. Threat to Idenitification: What if \(F\) also directly affects \(Y\)? (Note that there are no valid adjustment sets in this case)#
G4 = CausalGraph()
G4.add_node('Y', latent=False, pos=(4,0))
G4.add_node('D', latent=False, pos=(0,0))
G4.add_node('X', latent=False, pos=(2,-2))
G4.add_node("F", latent=True, pos=(0,-1))
G4.add_node("A", latent=True, pos=(-1,-1))
pos=nx.get_node_attributes(G4,'pos')
G4.add_edge("D", "Y")
G4.add_edge("X", "D")
G4.add_edge("F", "D")
G4.add_edge("A", "F")
G4.add_edge("A", "X")
G4.add_edge("A", "D")
G4.add_edge("F", "Y")
G4.add_edge("X", "Y")
nx.draw(G4, pos, with_labels = True, style = 'solid',
edge_color=['red' if G4.nodes[e[0]]['latent'] else 'gray' for e in G4.edges],
font_weight='bold', font_size=15, font_color='black',
node_color='white', arrowsize=30)
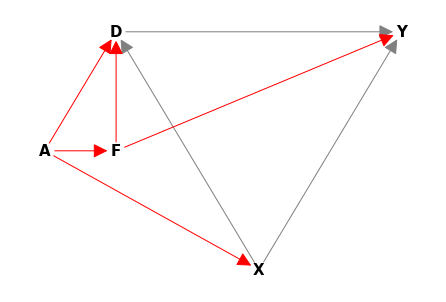
G4.optimal_minimal_adj_set("D", "Y", [], ["X"])
---------------------------------------------------------------------------
NoAdjException Traceback (most recent call last)
c:\Users\User\Machine_Learning\book_ml\Dags\Dags1.ipynb Celda 20 in <cell line: 1>()
----> <a href='vscode-notebook-cell:/c%3A/Users/User/Machine_Learning/book_ml/Dags/Dags1.ipynb#ch0000021?line=0'>1</a> G4.optimal_minimal_adj_set("D", "Y", [], ["X"])
File c:\Users\User\anaconda3\lib\site-packages\optimaladj\CausalGraph.py:393, in CausalGraph.optimal_minimal_adj_set(self, treatment, outcome, L, N)
390 H1 = self.build_H1(treatment, outcome, L, N)
392 if treatment in H1.neighbors(outcome):
--> 393 raise NoAdjException(EXCEPTION_NO_ADJ)
394 else:
395 optimal_minimal = self.unblocked(
396 H1, treatment, nx.node_boundary(H1, set([outcome]))
397 )
NoAdjException: An adjustment set formed by observable variables does not exist
This last code show us an error because there is no valid adustment set (among observed variables)
How can F affect Y directly? Is it reasonable?
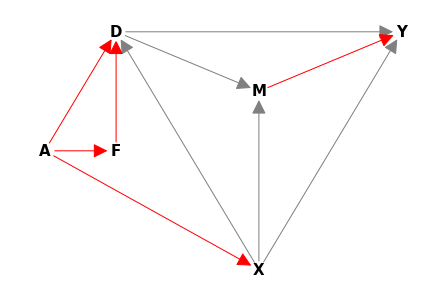
21.5. Introduce Match Amount \(M\) (very important mediator, why mediator?). \(M\) is not observed. Luckily adjusting for \(X\) still works if there is no \(F \to M\) arrow.#
G5 = CausalGraph()
G5.add_node('Y', latent=False, pos=(4,0))
G5.add_node('D', latent=False, pos=(0,0))
G5.add_node('X', latent=False, pos=(2,-2))
G5.add_node("F", latent=True, pos=(0,-1))
G5.add_node("A", latent=True, pos=(-1,-1))
G5.add_node("M", latent=True, pos=(2,-.5))
pos=nx.get_node_attributes(G5,'pos')
G5.add_edge("D", "Y")
G5.add_edge("X", "D")
G5.add_edge("F", "D")
G5.add_edge("A", "F")
G5.add_edge("A", "X")
G5.add_edge("A", "D")
G5.add_edge("D", "M")
G5.add_edge("M", "Y")
G5.add_edge("X", "M")
G5.add_edge("X", "Y")
print(G5.optimal_minimal_adj_set("D", "Y", [], ["X"]))
nx.draw(G5, pos, with_labels = True, style = 'solid',
edge_color=['red' if G5.nodes[e[0]]['latent'] else 'gray' for e in G5.edges],
font_weight='bold', font_size=15, font_color='black',
node_color='white', arrowsize=30)
{'X'}
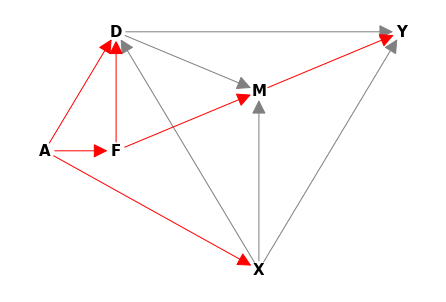
21.6. If there is \(F \to M\) arrow, then adjusting for \(X\) is not sufficient.#
G6 = CausalGraph()
G6.add_node('Y', latent=False, pos=(4,0))
G6.add_node('D', latent=False, pos=(0,0))
G6.add_node('X', latent=False, pos=(2,-2))
G6.add_node("F", latent=True, pos=(0,-1))
G6.add_node("A", latent=True, pos=(-1,-1))
G6.add_node("M", latent=True, pos=(2,-.5))
pos=nx.get_node_attributes(G6,'pos')
G6.add_edge("D", "Y")
G6.add_edge("X", "D")
G6.add_edge("F", "D")
G6.add_edge("A", "F")
G6.add_edge("A", "X")
G6.add_edge("D", "M")
G6.add_edge("F", "M")
G6.add_edge("A", "D")
G6.add_edge("M", "Y")
G6.add_edge("X", "M")
G6.add_edge("X", "Y")
nx.draw(G6, pos, with_labels = True, style = 'solid',
edge_color=['red' if G6.nodes[e[0]]['latent'] else 'gray' for e in G6.edges],
font_weight='bold', font_size=15, font_color='black',
node_color='white', arrowsize=30)
G6.optimal_minimal_adj_set("D", "Y", [], ["X"])
---------------------------------------------------------------------------
NoAdjException Traceback (most recent call last)
c:\Users\User\Machine_Learning\book_ml\Dags\Dags1.ipynb Celda 27 in <cell line: 1>()
----> <a href='vscode-notebook-cell:/c%3A/Users/User/Machine_Learning/book_ml/Dags/Dags1.ipynb#ch0000029?line=0'>1</a> G6.optimal_minimal_adj_set("D", "Y", [], ["X"])
File c:\Users\User\anaconda3\lib\site-packages\optimaladj\CausalGraph.py:393, in CausalGraph.optimal_minimal_adj_set(self, treatment, outcome, L, N)
390 H1 = self.build_H1(treatment, outcome, L, N)
392 if treatment in H1.neighbors(outcome):
--> 393 raise NoAdjException(EXCEPTION_NO_ADJ)
394 else:
395 optimal_minimal = self.unblocked(
396 H1, treatment, nx.node_boundary(H1, set([outcome]))
397 )
NoAdjException: An adjustment set formed by observable variables does not exist
This last code show us an error because there is no valid adustment set (among observed variables)


