7. Linear Penalized Regs#
7.1. Data Generating Process: Approximately Sparse#
install.packages("librarian", quiet = T)
librarian::shelf(glmnet, broom, tidyverse, hdm, quiet = T)
set.seed(1)
n = 100;
p = 400;
Z= runif(n)-1/2;
W = matrix(runif(n*p)-1/2, n, p);
beta = 1/seq(1:p)^2; # approximately sparse beta
#beta = rnorm(p)*.2 # dense beta
gX = exp(4*Z)+ W%*%beta; # leading term nonlinear
X = cbind(Z, Z^2, Z^3, W ); # polynomials in Zs will be approximating exp(4*Z)
Y = gX + rnorm(n); #generate Y
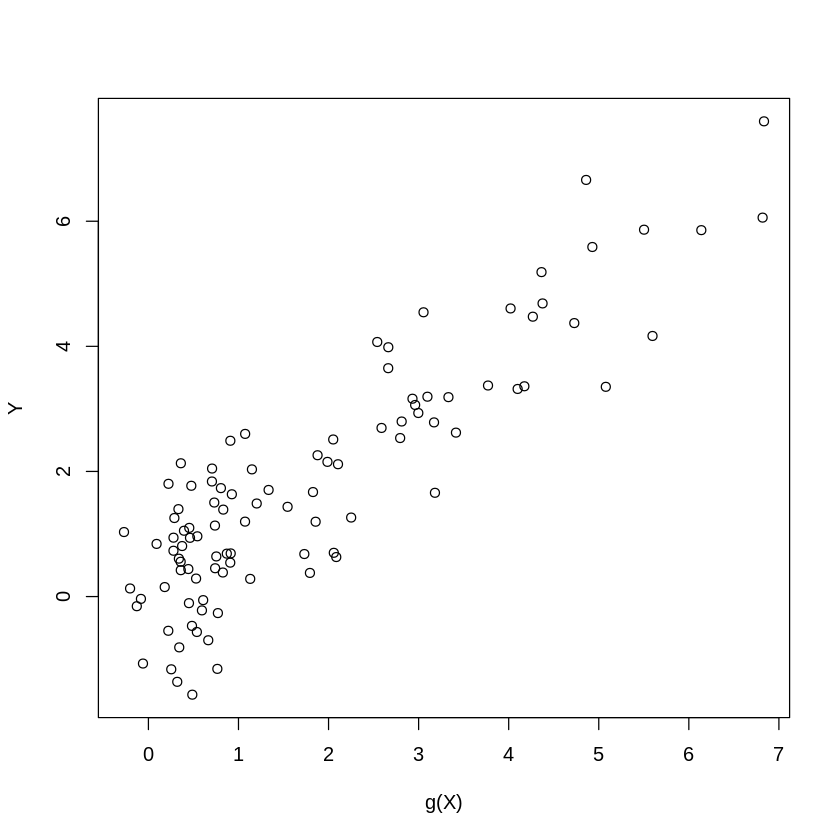
plot(gX,Y, xlab="g(X)", ylab="Y") #plot V vs g(X)
print(c("theoretical R2:", var(gX)/var(Y)))
Warning message in system("timedatectl", intern = TRUE):
“running command 'timedatectl' had status 1”
[1] "theoretical R2:" "0.826881788964026"
| 0.8268818 |
We use package Glmnet to carry out predictions using cross-validated lasso, ridge, and elastic net
# library(glmnet)
fit.lasso.cv <- cv.glmnet(X, Y, family="gaussian", alpha=1) # family gaussian means that we'll be using square loss
fit.ridge <- cv.glmnet(X, Y, family="gaussian", alpha=0) # family gaussian means that we'll be using square loss
fit.elnet <- cv.glmnet(X, Y, family="gaussian", alpha=.5) # family gaussian means that we'll be using square loss
yhat.lasso.cv <- predict(fit.lasso.cv, newx = X) # predictions
yhat.ridge <- predict(fit.ridge, newx = X)
yhat.elnet <- predict(fit.elnet, newx = X)
MSE.lasso.cv <- summary(lm((gX-yhat.lasso.cv)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.ridge <- summary(lm((gX-yhat.ridge)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.elnet <- summary(lm((gX-yhat.elnet)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
Here we compute the lasso and ols post lasso using plug-in choices for penalty levels, using package hdm
# library(hdm)
fit.rlasso <- rlasso(Y~X, post=FALSE) # lasso with plug-in penalty level
fit.rlasso.post <- rlasso(Y~X, post=TRUE) # post-lasso with plug-in penalty level
yhat.rlasso <- predict(fit.rlasso) #predict g(X) for values of X
yhat.rlasso.post <- predict(fit.rlasso.post) #predict g(X) for values of X
MSE.lasso <- summary(lm((gX-yhat.rlasso)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.lasso.post <- summary(lm((gX-yhat.rlasso.post)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
Next we code up lava, which alternates the fitting of lasso and ridge
# library(glmnet)
lava.predict<- function(X,Y, iter=5){
g1 = predict(rlasso(X, Y, post=F)) #lasso step fits "sparse part"
m1 = predict(glmnet(X, as.vector(Y - g1), family = "gaussian", alpha = 0, lambda = 20),newx=X ) #ridge step fits the "dense" part
i = 1
while(i <= iter) {
g1 = predict(rlasso(X, as.vector(Y - m1), post = F)) #lasso step fits "sparse part"
m1 = predict(glmnet(X, as.vector(Y - g1), family = "gaussian", alpha = 0, lambda = 20),newx = X ) #ridge step fits the "dense" part
i = i+1
}
return(g1+m1)
}
yhat.lava = lava.predict(X,Y)
MSE.lava <- summary(lm((gX-yhat.lava)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.lava
- 0.158968193469853
- 0.0256845068490924
# library(xtable)
table<- matrix(0, 6, 2)
table[1,1:2] <- MSE.lasso.cv
table[2,1:2] <- MSE.ridge
table[3,1:2] <- MSE.elnet
table[4,1:2] <- MSE.lasso
table[5,1:2] <- MSE.lasso.post
table[6,1:2] <- MSE.lava
colnames(table)<- c("MSA", "S.E. for MSA")
rownames(table)<- c("Cross-Validated Lasso", "Cross-Validated ridge","Cross-Validated elnet",
"Lasso","Post-Lasso","Lava")
# tab <- xtable(table, digits =3)
table
| MSA | S.E. for MSA | |
|---|---|---|
| Cross-Validated Lasso | 0.3666009 | 0.061279916 |
| Cross-Validated ridge | 2.3842559 | 0.369909988 |
| Cross-Validated elnet | 0.3988608 | 0.063757962 |
| Lasso | 0.1482190 | 0.026705771 |
| Post-Lasso | 0.0845236 | 0.009469643 |
| Lava | 0.1589682 | 0.025684507 |
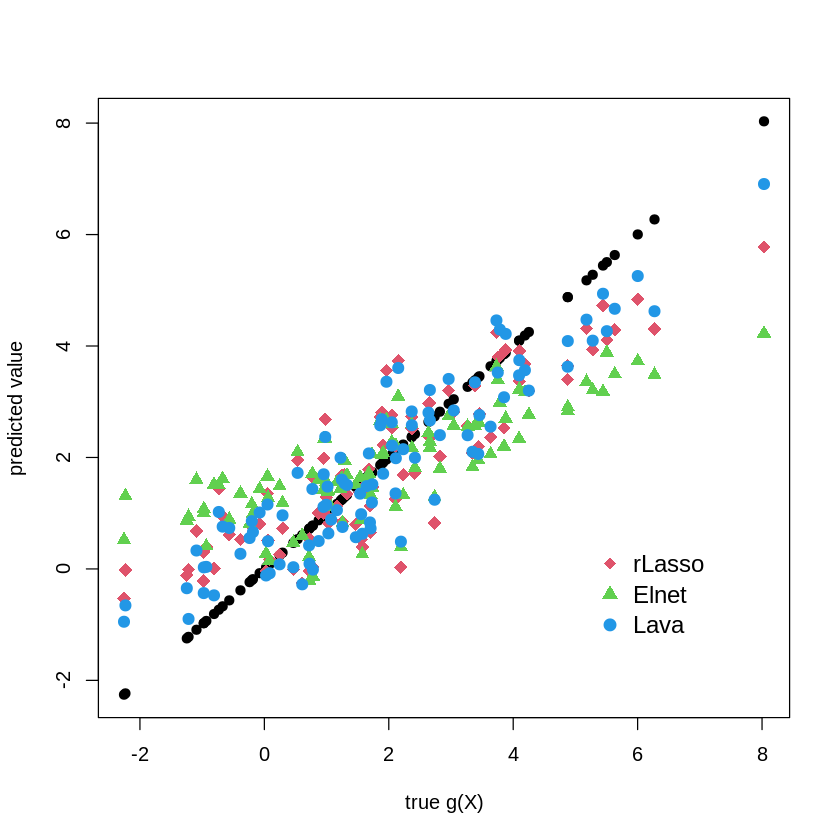
plot(gX, gX, pch=19, cex=1, ylab="predicted value", xlab="true g(X)")
points(gX, yhat.rlasso, col=2, pch=18, cex = 1.5 )
points(gX, yhat.rlasso.post, col=3, pch=17, cex = 1.2 )
points( gX, yhat.lasso.cv,col=4, pch=19, cex = 1.2 )
legend("bottomright",
legend = c("rLasso", "Post-rLasso", "CV Lasso"),
col = c(2,3,4),
pch = c(18,17, 19),
bty = "n",
pt.cex = 1.3,
cex = 1.2,
text.col = "black",
horiz = F ,
inset = c(0.1, 0.1))
7.2. Data Generating Process: Approximately Sparse + Small Dense Part#
set.seed(1)
n = 100;
p = 400;
Z= runif(n)-1/2;
W = matrix(runif(n*p)-1/2, n, p);
beta = rnorm(p)*.2 # dense beta
gX = exp(4*Z)+ W%*%beta; # leading term nonlinear
X = cbind(Z, Z^2, Z^3, W ); # polynomials in Zs will be approximating exp(4*Z)
Y = gX + rnorm(n); #generate Y
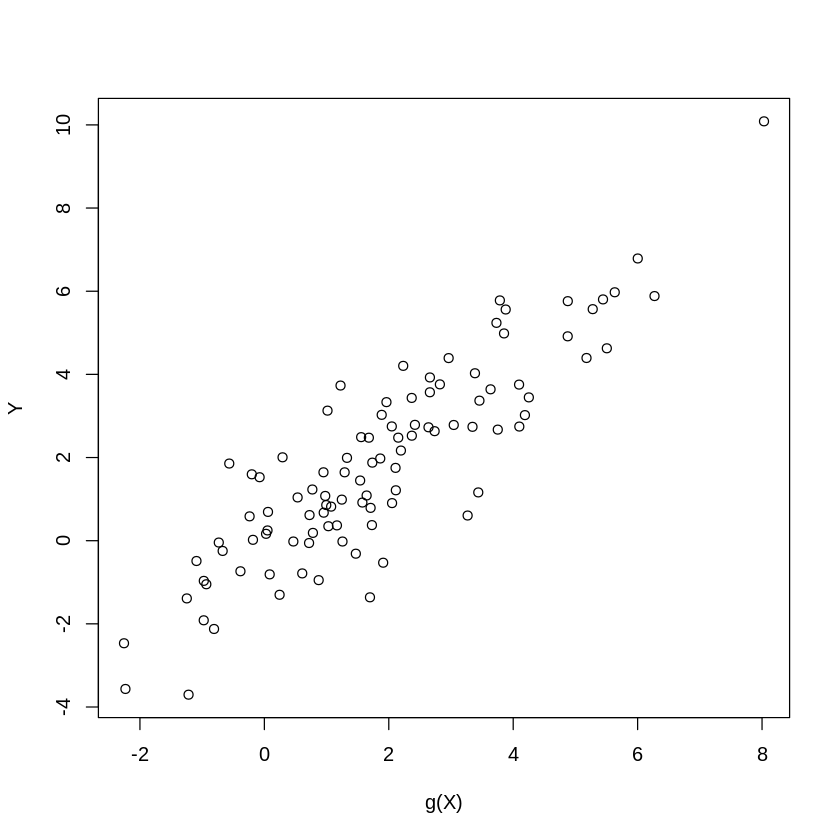
plot(gX,Y, xlab="g(X)", ylab="Y") #plot V vs g(X)
print( c("theoretical R2:", var(gX)/var(Y)))
[1] "theoretical R2:" "0.696687990094227"
| 0.696688 |
# library(glmnet)
fit.lasso.cv <- cv.glmnet(X, Y, family="gaussian", alpha=1) # family gaussian means that we'll be using square loss
fit.ridge <- cv.glmnet(X, Y, family="gaussian", alpha=0) # family gaussian means that we'll be using square loss
fit.elnet <- cv.glmnet(X, Y, family="gaussian", alpha=.5) # family gaussian means that we'll be using square loss
yhat.lasso.cv <- predict(fit.lasso.cv, newx = X) # predictions
yhat.ridge <- predict(fit.ridge, newx = X)
yhat.elnet <- predict(fit.elnet, newx = X)
MSE.lasso.cv <- summary(lm((gX-yhat.lasso.cv)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.ridge <- summary(lm((gX-yhat.ridge)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.elnet <- summary(lm((gX-yhat.elnet)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
# library(hdm)
fit.rlasso <- rlasso(Y~X, post=FALSE) # lasso with plug-in penalty level
fit.rlasso.post <- rlasso(Y~X, post=TRUE) # post-lasso with plug-in penalty level
yhat.rlasso <- predict(fit.rlasso) #predict g(X) for values of X
yhat.rlasso.post <- predict(fit.rlasso.post) #predict g(X) for values of X
MSE.lasso <- summary(lm((gX-yhat.rlasso)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.lasso.post <- summary(lm((gX-yhat.rlasso.post)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
# library(glmnet)
lava.predict<- function(X,Y, iter=5){
g1 = predict(rlasso(X, Y, post=F)) #lasso step fits "sparse part"
m1 = predict(glmnet(X, as.vector(Y-g1), family="gaussian", alpha=0, lambda =20),newx=X ) #ridge step fits the "dense" part
i=1
while(i<= iter) {
g1 = predict(rlasso(X, as.vector(Y-m1), post=F)) #lasso step fits "sparse part"
m1 = predict(glmnet(X, as.vector(Y-g1), family="gaussian", alpha=0, lambda =20),newx=X ); #ridge step fits the "dense" part
i = i+1
}
return(g1+m1);
}
yhat.lava = lava.predict(X,Y)
MSE.lava <- summary(lm((gX-yhat.lava)^2~1))$coef[1:2] # report MSE and standard error for MSE for approximating g(X)
MSE.lava
- 0.679714730890029
- 0.0737496772656864
# library(xtable)
table<- matrix(0, 6, 2)
table[1,1:2] <- MSE.lasso.cv
table[2,1:2] <- MSE.ridge
table[3,1:2] <- MSE.elnet
table[4,1:2] <- MSE.lasso
table[5,1:2] <- MSE.lasso.post
table[6,1:2] <- MSE.lava
colnames(table)<- c("MSA", "S.E. for MSA")
rownames(table)<- c("Cross-Validated Lasso", "Cross-Validated ridge","Cross-Validated elnet",
"Lasso","Post-Lasso","Lava")
# tab <- xtable(table, digits =3)
table
| MSA | S.E. for MSA | |
|---|---|---|
| Cross-Validated Lasso | 1.9318225 | 0.29130485 |
| Cross-Validated ridge | 3.4106685 | 0.49426500 |
| Cross-Validated elnet | 1.8251591 | 0.25189955 |
| Lasso | 0.9641151 | 0.11978038 |
| Post-Lasso | 1.5966018 | 0.20707956 |
| Lava | 0.6797147 | 0.07374968 |
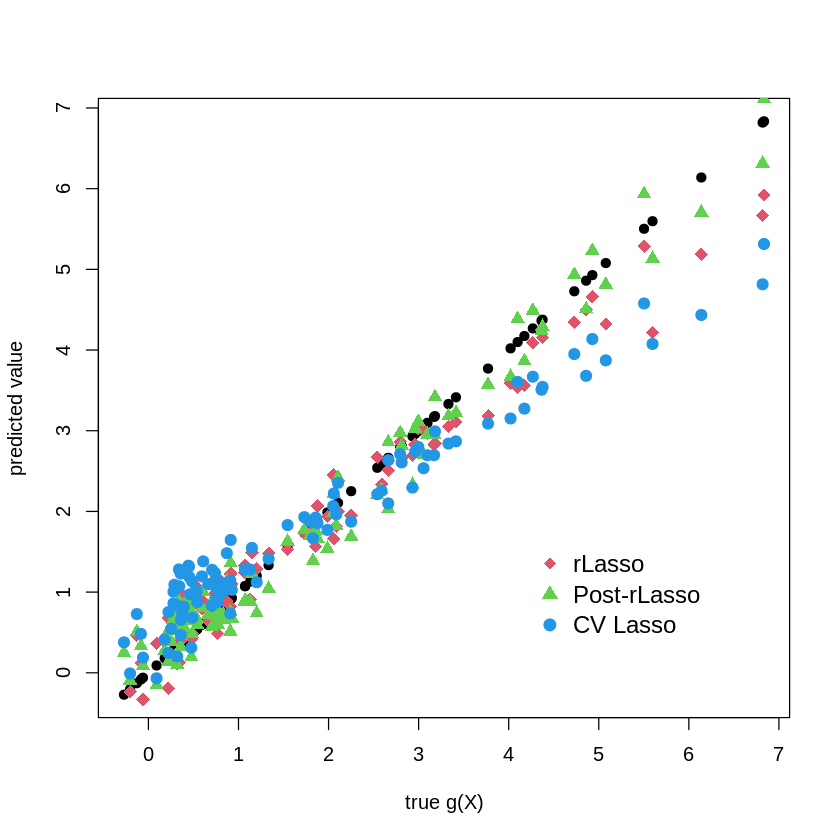
plot(gX, gX, pch=19, cex=1, ylab="predicted value", xlab="true g(X)")
points(gX, yhat.rlasso, col=2, pch=18, cex = 1.5 )
points(gX, yhat.elnet, col=3, pch=17, cex = 1.2 )
points(gX, yhat.lava, col=4, pch=19, cex = 1.2 )
legend("bottomright",
legend = c("rLasso", "Elnet", "Lava"),
col = c(2,3,4),
pch = c(18,17, 19),
bty = "n",
pt.cex = 1.3,
cex = 1.2,
text.col = "black",
horiz = F ,
inset = c(0.1, 0.1))