9. Experiment on orthogonal Learning

9.1. Simulation Design 2

# install.packages("librarian", quiet = T)
librarian::shelf(hdm, quiet = T)

set.seed(1)
B= 100 # trials
Naive = rep(0, B)
Orthogonal = rep(0, B)

for (i in 1:B){
    
  n = 10000
  p = 100
  beta = 1 / (1:p)^2
  gamma =1 / (1:p)^2

  X = matrix(rnorm(n*p), n, p)


  D = X%*%gamma + rnorm(n)/4

  Y = D + X%*%beta + rnorm(n)

  # single selection method

  SX.IDs = which(rlasso(Y~ D+X)$coef[-c(1,2)] !=0)  #select covariates by Lasso


  if (sum(SX.IDs)==0) {Naive[i] = lm(Y~ D)$coef[2]}

  if (sum(SX.IDs)>0) {Naive[i] = lm(Y~ D + X[,SX.IDs])$coef[2]}



  #partialling out

  resY = rlasso(Y~ X, Post=F)$res
  resD = rlasso(D~ X, Post=F)$res
  Orthogonal[i]= lm(resY ~ resD)$coef[2]

}

Installing package into ‘/usr/local/lib/R/site-library’
(as ‘lib’ is unspecified)

also installing the dependency ‘BiocManager’



  These packages will be installed:

  'hdm'

  It may take some time.

also installing the dependencies ‘iterators’, ‘foreach’, ‘shape’, ‘Rcpp’, ‘RcppEigen’, ‘glmnet’, ‘checkmate’, ‘Formula’

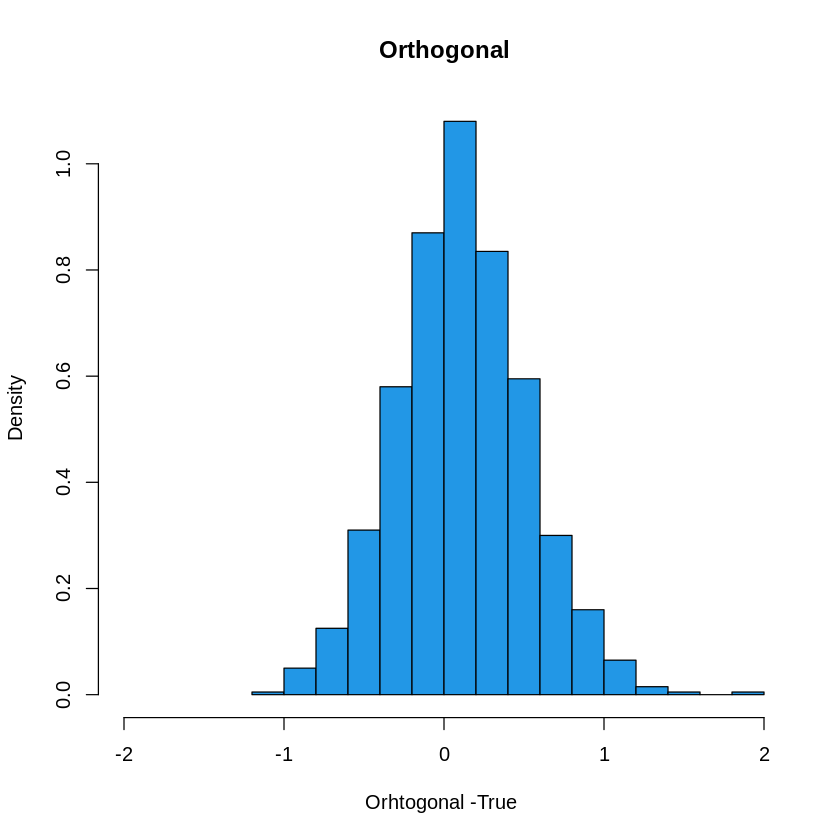
hist(Orthogonal-1,col=4, freq=F, xlim= c(-2, 2), xlab= "Orhtogonal -True ", main="Orthogonal")
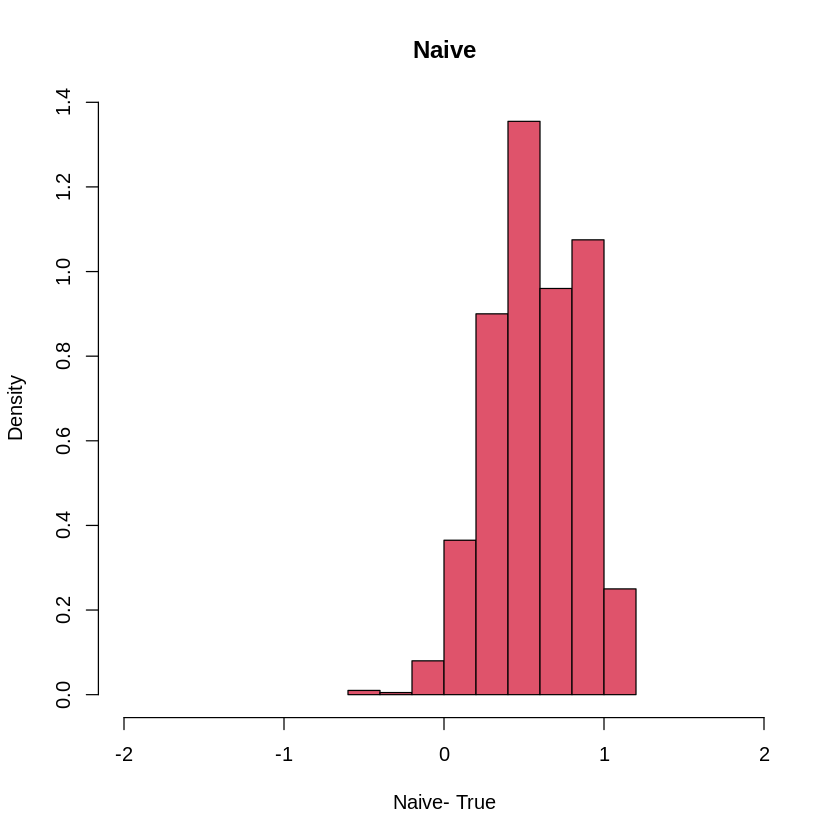
hist(Naive-1, col=2, freq=F, xlim= c(-2,2), xlab= "Naive- True", main = "Naive")

9.2. Simulation Design 2

# library(hdm)

set.seed(1)
B= 1000 # trials 
Naive = rep(0, B)
Orthogonal = rep(0, B)

for (i in 1:B){
      
  n =100
  p = 100
  beta = 1/(1:p)^2
  gamma = 1/(1:p)^2

  X = matrix(rnorm(n*p), n, p)
      
      
  D = X%*%gamma + rnorm(n)/4

  Y = D+ X%*%beta + rnorm(n)

  # single selection method

  SX.IDs = which(rlasso(Y~ D+X)$coef[-c(1,2)] !=0)  #select covariates by Lasso


  if (sum(SX.IDs)==0) {Naive[i] = lm(Y~ D)$coef[2]}

  if (sum(SX.IDs)>0) {Naive[i] = lm(Y~ D + X[,SX.IDs])$coef[2]}

  #partialling out

  resY = rlasso(Y~ X, Post=T)$res
  resD = rlasso(D~ X, Post=T)$res
  Orthogonal[i]= lm(resY ~ resD)$coef[2]

}

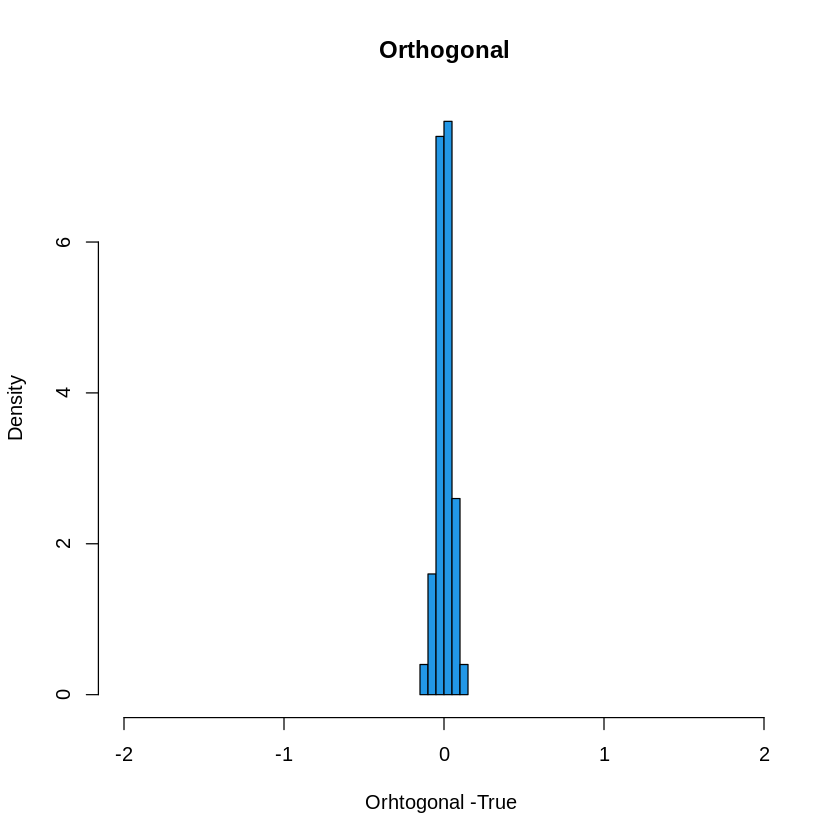
hist(Orthogonal-1,col=4, freq=F, xlim= c(-2, 2), xlab= "Orhtogonal -True ", main="Orthogonal")
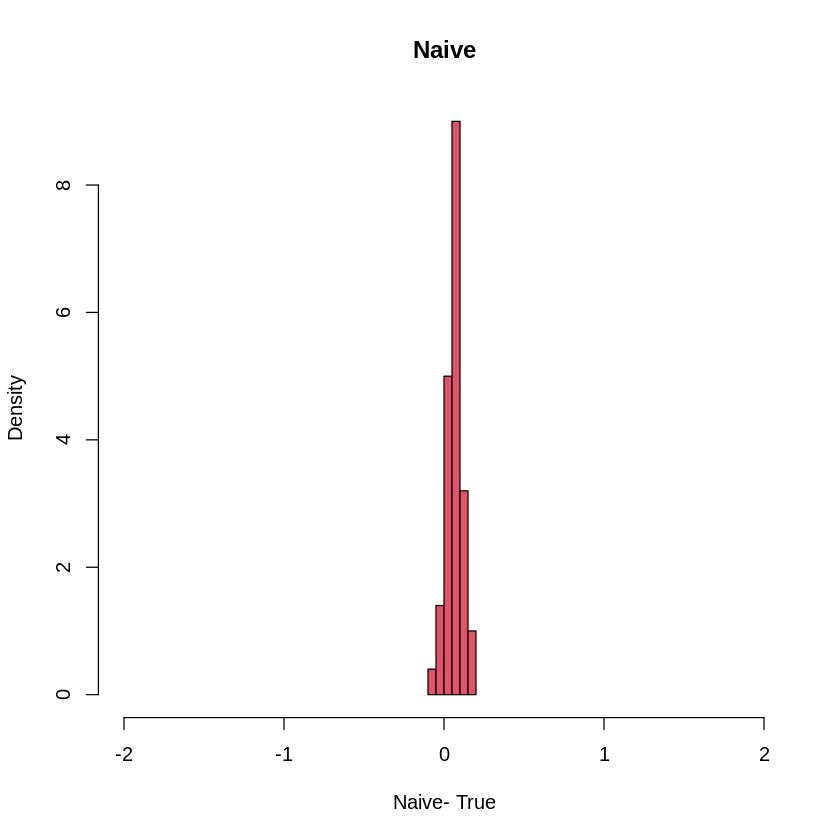
hist(Naive-1, col=2, freq=F, xlim= c(-2,2), xlab= "Naive- True", main = "Naive")