14. AutoML for wage prediction#
We illustrate how to predict an outcome variable Y in a high-dimensional setting, using the AutoML package H2O that covers the complete pipeline from the raw dataset to the deployable machine learning model. In last few years, AutoML or automated machine learning has become widely popular among data science community. Again, re-analyse the wage prediction problem using data from the U.S. March Supplement of the Current Population Survey (CPS) in 2015.
We can use AutoML as a benchmark and compare it to the methods that we used in the previous notebook where we applied one machine learning method after the other.
# load the H2O package
install.packages("librarian", quiet = T)
librarian::shelf(h2o, tidyverse, quiet = T)
# library(h2o)
Warning message in system("timedatectl", intern = TRUE):
“running command 'timedatectl' had status 1”
# load the data set
data = read_csv("https://github.com/alexanderquispe/14.38_Causal_ML/raw/main/data/wage2015_subsample_inference.csv", show_col_types = F)
# split the data
set.seed(1234)
training <- sample(nrow(data), nrow(data)*(3/4), replace=FALSE)
train <- data[training,]
test <- data[-training,]
# start h2o cluster
h2o.init()
H2O is not running yet, starting it now...
Note: In case of errors look at the following log files:
/tmp/Rtmp04tHzQ/file3c5628322d/h2o_UnknownUser_started_from_r.out
/tmp/Rtmp04tHzQ/file3c7321dc6f/h2o_UnknownUser_started_from_r.err
Starting H2O JVM and connecting: .... Connection successful!
R is connected to the H2O cluster:
H2O cluster uptime: 2 seconds 645 milliseconds
H2O cluster timezone: Etc/UTC
H2O data parsing timezone: UTC
H2O cluster version: 3.36.1.2
H2O cluster version age: 1 month and 23 days
H2O cluster name: H2O_started_from_R_root_tlg556
H2O cluster total nodes: 1
H2O cluster total memory: 3.17 GB
H2O cluster total cores: 2
H2O cluster allowed cores: 2
H2O cluster healthy: TRUE
H2O Connection ip: localhost
H2O Connection port: 54321
H2O Connection proxy: NA
H2O Internal Security: FALSE
R Version: R version 4.2.0 (2022-04-22)
# convert data as h2o type
train_h = as.h2o(train)
test_h = as.h2o(test)
# have a look at the data
h2o.describe(train_h)
|======================================================================| 100%
|======================================================================| 100%
| Label | Type | Missing | Zeros | PosInf | NegInf | Min | Max | Mean | Sigma | Cardinality |
|---|---|---|---|---|---|---|---|---|---|---|
| <chr> | <chr> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| rownames | int | 0 | 0 | 0 | 0 | 10.000000 | 3.264300e+04 | 1.560586e+04 | 9.721144e+03 | NA |
| wage | real | 0 | 0 | 0 | 0 | 3.021978 | 5.288457e+02 | 2.337760e+01 | 2.060944e+01 | NA |
| lwage | real | 0 | 0 | 0 | 0 | 1.105912 | 6.270697e+00 | 2.969673e+00 | 5.721780e-01 | NA |
| sex | int | 0 | 2115 | 0 | 0 | 0.000000 | 1.000000e+00 | 4.523563e-01 | 4.977894e-01 | NA |
| shs | int | 0 | 3770 | 0 | 0 | 0.000000 | 1.000000e+00 | 2.382185e-02 | 1.525136e-01 | NA |
| hsg | int | 0 | 2896 | 0 | 0 | 0.000000 | 1.000000e+00 | 2.501295e-01 | 4.331435e-01 | NA |
| scl | int | 0 | 2795 | 0 | 0 | 0.000000 | 1.000000e+00 | 2.762817e-01 | 4.472157e-01 | NA |
| clg | int | 0 | 2646 | 0 | 0 | 0.000000 | 1.000000e+00 | 3.148628e-01 | 4.645213e-01 | NA |
| ad | int | 0 | 3341 | 0 | 0 | 0.000000 | 1.000000e+00 | 1.349042e-01 | 3.416654e-01 | NA |
| mw | int | 0 | 2872 | 0 | 0 | 0.000000 | 1.000000e+00 | 2.563439e-01 | 4.366704e-01 | NA |
| so | int | 0 | 2707 | 0 | 0 | 0.000000 | 1.000000e+00 | 2.990678e-01 | 4.579089e-01 | NA |
| we | int | 0 | 3034 | 0 | 0 | 0.000000 | 1.000000e+00 | 2.143967e-01 | 4.104563e-01 | NA |
| ne | int | 0 | 2973 | 0 | 0 | 0.000000 | 1.000000e+00 | 2.301916e-01 | 4.210099e-01 | NA |
| exp1 | real | 0 | 49 | 0 | 0 | 0.000000 | 4.700000e+01 | 1.385590e+01 | 1.067133e+01 | NA |
| exp2 | real | 0 | 49 | 0 | 0 | 0.000000 | 2.209000e+01 | 3.058340e+00 | 4.039614e+00 | NA |
| exp3 | real | 0 | 49 | 0 | 0 | 0.000000 | 1.038230e+02 | 8.385453e+00 | 1.465866e+01 | NA |
| exp4 | real | 0 | 49 | 0 | 0 | 0.000000 | 4.879681e+02 | 2.566770e+01 | 5.425545e+01 | NA |
| occ | int | 0 | 0 | 0 | 0 | 10.000000 | 1.000000e+05 | 5.247124e+03 | 1.157852e+04 | NA |
| occ2 | int | 0 | 0 | 0 | 0 | 1.000000 | 2.200000e+01 | 1.168514e+01 | 6.965247e+00 | NA |
| ind | int | 0 | 0 | 0 | 0 | 370.000000 | 1.000000e+05 | 6.605252e+03 | 5.173314e+03 | NA |
| ind2 | int | 0 | 0 | 0 | 0 | 2.000000 | 2.200000e+01 | 1.329777e+01 | 5.691808e+00 | NA |
# define the variables
y = 'lwage'
x = setdiff(names(data), c('wage','occ2', 'ind2'))
# run AutoML for 10 base models and a maximal runtime of 100 seconds
aml = h2o.automl(x=x,y = y,
training_frame = train_h,
leaderboard_frame = test_h,
max_models = 10,
seed = 1,
max_runtime_secs = 100
)
# AutoML Leaderboard
lb = aml@leaderboard
print(lb, n = nrow(lb))
Warning message in .verify_dataxy(training_frame, x, y):
“removing response variable from the explanatory variables”
|======================================================================| 100%
model_id rmse mse
1 StackedEnsemble_AllModels_1_AutoML_1_20220719_171824 0.4669942 0.2180836
2 StackedEnsemble_BestOfFamily_1_AutoML_1_20220719_171824 0.4690110 0.2199713
3 GBM_1_AutoML_1_20220719_171824 0.4709260 0.2217713
4 GBM_2_AutoML_1_20220719_171824 0.4724988 0.2232551
5 GBM_3_AutoML_1_20220719_171824 0.4733774 0.2240862
6 GBM_4_AutoML_1_20220719_171824 0.4740358 0.2247100
7 XGBoost_3_AutoML_1_20220719_171824 0.4791050 0.2295416
8 XRT_1_AutoML_1_20220719_171824 0.4884560 0.2385893
9 DRF_1_AutoML_1_20220719_171824 0.4893117 0.2394260
10 XGBoost_2_AutoML_1_20220719_171824 0.5039629 0.2539786
11 XGBoost_1_AutoML_1_20220719_171824 0.5065185 0.2565610
12 GLM_1_AutoML_1_20220719_171824 0.5159068 0.2661599
mae rmsle mean_residual_deviance
1 0.3479339 0.1176141 0.2180836
2 0.3495583 0.1182146 0.2199713
3 0.3513555 0.1186738 0.2217713
4 0.3540236 0.1189309 0.2232551
5 0.3518737 0.1190304 0.2240862
6 0.3529919 0.1193677 0.2247100
7 0.3582960 0.1207383 0.2295416
8 0.3666487 0.1229990 0.2385893
9 0.3663660 0.1233622 0.2394260
10 0.3757325 0.1267305 0.2539786
11 0.3788916 0.1275746 0.2565610
12 0.3932883 0.1298952 0.2661599
[12 rows x 6 columns]
We see that two Stacked Ensembles are at the top of the leaderboard. Stacked Ensembles often outperform a single model. The out-of-sample (test) MSE of the leading model is given by
aml@leaderboard$mse[1]
mse
1 0.2180836
[1 row x 1 column]
The in-sample performance can be evaluated by
aml@leader
Model Details:
==============
H2ORegressionModel: stackedensemble
Model ID: StackedEnsemble_AllModels_1_AutoML_1_20220719_171824
Number of Base Models: 10
Base Models (count by algorithm type):
drf gbm glm xgboost
2 4 1 3
Metalearner:
Metalearner algorithm: glm
Metalearner cross-validation fold assignment:
Fold assignment scheme: AUTO
Number of folds: 5
Fold column: NULL
Metalearner hyperparameters:
H2ORegressionMetrics: stackedensemble
** Reported on training data. **
MSE: 0.1415518
RMSE: 0.3762337
MAE: 0.2857554
RMSLE: 0.09723326
Mean Residual Deviance : 0.1415518
H2ORegressionMetrics: stackedensemble
** Reported on cross-validation data. **
** 5-fold cross-validation on training data (Metrics computed for combined holdout predictions) **
MSE: 0.219355
RMSE: 0.4683535
MAE: 0.3549446
RMSLE: 0.1199425
Mean Residual Deviance : 0.219355
Cross-Validation Metrics Summary:
mean sd cv_1_valid cv_2_valid cv_3_valid
mae 0.354820 0.014198 0.347980 0.337307 0.369668
mean_residual_deviance 0.219562 0.023919 0.205474 0.190237 0.236612
mse 0.219562 0.023919 0.205474 0.190237 0.236612
null_deviance 253.053390 27.814274 228.977890 252.801100 267.446900
r2 0.327839 0.035450 0.301765 0.389207 0.310545
residual_deviance 169.472760 18.989317 159.447500 154.282040 183.847530
rmse 0.468019 0.025515 0.453292 0.436161 0.486428
rmsle 0.119856 0.006879 0.117210 0.110752 0.122937
cv_4_valid cv_5_valid
mae 0.369248 0.349898
mean_residual_deviance 0.249945 0.215545
mse 0.249945 0.215545
null_deviance 291.623540 224.417530
r2 0.326576 0.311102
residual_deviance 195.456850 154.329910
rmse 0.499945 0.464268
rmsle 0.129307 0.119074
This is in line with our previous results. To understand how the ensemble works, let’s take a peek inside the Stacked Ensemble “All Models” model. The “All Models” ensemble is an ensemble of all of the individual models in the AutoML run. This is often the top performing model on the leaderboard.
model_ids <- as.data.frame(aml@leaderboard$model_id)[,1]
# Get the "All Models" Stacked Ensemble model
se <- h2o.getModel(grep("StackedEnsemble_AllModels", model_ids, value = TRUE)[1])
# Get the Stacked Ensemble metalearner model
metalearner <- se@model$metalearner_model
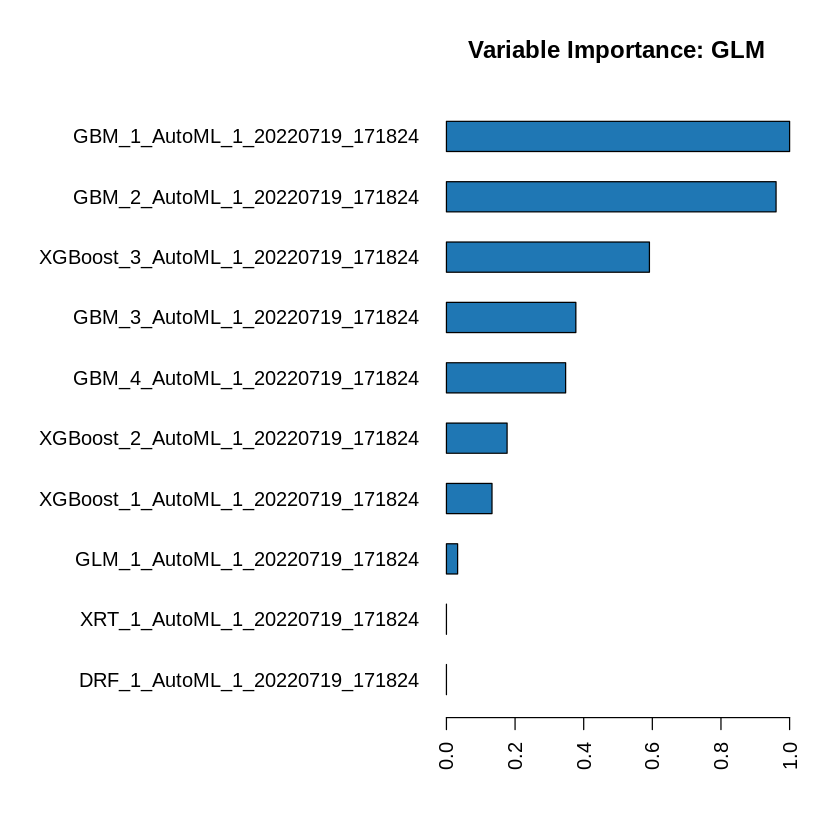
h2o.varimp(metalearner)
| variable | relative_importance | scaled_importance | percentage |
|---|---|---|---|
| <chr> | <dbl> | <dbl> | <dbl> |
| GBM_1_AutoML_1_20220719_171824 | 0.092798688 | 1.00000000 | 0.276345757 |
| GBM_2_AutoML_1_20220719_171824 | 0.089138567 | 0.96055849 | 0.265446264 |
| XGBoost_3_AutoML_1_20220719_171824 | 0.054892909 | 0.59152678 | 0.163465916 |
| GBM_3_AutoML_1_20220719_171824 | 0.034995779 | 0.37711503 | 0.104214137 |
| GBM_4_AutoML_1_20220719_171824 | 0.032231744 | 0.34732974 | 0.095983101 |
| XGBoost_2_AutoML_1_20220719_171824 | 0.016404439 | 0.17677447 | 0.048850875 |
| XGBoost_1_AutoML_1_20220719_171824 | 0.012321778 | 0.13277965 | 0.036693094 |
| GLM_1_AutoML_1_20220719_171824 | 0.003022545 | 0.03257099 | 0.009000855 |
| XRT_1_AutoML_1_20220719_171824 | 0.000000000 | 0.00000000 | 0.000000000 |
| DRF_1_AutoML_1_20220719_171824 | 0.000000000 | 0.00000000 | 0.000000000 |
The table above gives us the variable importance of the metalearner in the ensemble. The AutoML Stacked Ensembles use the default metalearner algorithm (GLM with non-negative weights), so the variable importance of the metalearner is actually the standardized coefficient magnitudes of the GLM.
h2o.varimp_plot(metalearner)
14.1. Generating Predictions Using Leader Model#
We can also generate predictions on a test sample using the leader model object.
pred <- as.matrix(h2o.predict(aml@leader,test_h)) # make prediction using x data from the test sample
head(pred)
|======================================================================| 100%
| predict |
|---|
| 3.028706 |
| 2.533245 |
| 2.823822 |
| 2.470121 |
| 2.776539 |
| 2.678759 |
This allows us to estimate the out-of-sample (test) MSE and the standard error as well.
y_test <- as.matrix(test_h$lwage)
summary(lm((y_test-pred)^2~1))$coef[1:2]
- 0.218083617310276
- 0.0149540081481586
We observe both a lower MSE and a lower standard error compared to our previous results (see here).
h2o.shutdown(prompt = F)


